题目内容
函数y=3x2-x+2(0≤x≤1)的值域为 .
【答案】分析:利用二次函数的单调性即可求出值域.
解答:解:∵函数y=f(x)=3x2-x+2=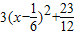 ,(0≤x≤1),
,(0≤x≤1),
∴此函数y在区间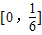 是单调递减,在区间
是单调递减,在区间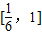 是单调递增;
是单调递增;
∴f(x)的最小值=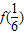 =
=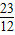 ,而f(0)=2,f(1)=4;
,而f(0)=2,f(1)=4;
∴函数f(x)的值域为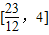 .
.
故答案为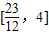 .
.
点评:熟练掌握二次函数的单调性是解题解题的关键.
解答:解:∵函数y=f(x)=3x2-x+2=
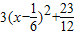 ,(0≤x≤1),
,(0≤x≤1),∴此函数y在区间
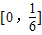 是单调递减,在区间
是单调递减,在区间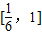 是单调递增;
是单调递增;∴f(x)的最小值=
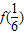 =
=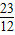 ,而f(0)=2,f(1)=4;
,而f(0)=2,f(1)=4;∴函数f(x)的值域为
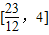 .
.故答案为
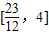 .
.点评:熟练掌握二次函数的单调性是解题解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目