题目内容
设锐角三角形ABC的内角A、B、C的对边分别为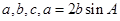 .
.
(1)求角B的大小;
(2)若a=3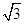 ,c=5,求b.
,c=5,求b.
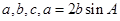 .
.(1)求角B的大小;
(2)若a=3
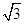 ,c=5,求b.
,c=5,求b.(1)  ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)根据正弦定理:

 ,代入到
,代入到 ,解得
,解得 的值,从而求出角B的大小;
的值,从而求出角B的大小;(2)由(1)的结果知
 ,结合余弦定理知
,结合余弦定理知 可求
可求 的值.
的值.试题解析:解(1)由a=2bsin A,根据正弦定理得
sin A=2sin Bsin A,所以sin B=
 .
.由△ABC为锐角三角形,得B=
 .
.(2)根据余弦定理,得
b2=a2+c2-2accos B=27+25-45=7,
所以b=
 .
.
练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 .
. ,n
,n ,试求|m
,试求|m n|的最小值.
n|的最小值. 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 .
. 的值;(2)若
的值;(2)若 ,求
,求 的取值范围.
的取值范围.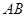 的中点,点D,E分别在半径OA,OB上.若
的中点,点D,E分别在半径OA,OB上.若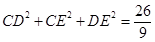 ,则
,则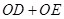 的最大值是 .
的最大值是 . ,则三角形△ABC为( ).
,则三角形△ABC为( ).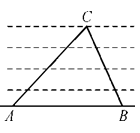
 中,角
中,角 所对的边分别为
所对的边分别为 ,
, ,
, ,
, ,则
,则 .
. 中,已知
中,已知 ,
, ,则B等于( )
,则B等于( )

