题目内容
已知向量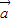 =(1,m+2),
=(1,m+2),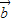 =(m,-1),且
=(m,-1),且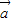 ∥
∥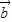 ,则|
,则|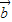 |等于( )
|等于( )A.
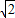
B.2
C.
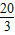
D.
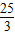
【答案】分析:根据题意,由结合向量平行的坐标表示方法,解可得m的值,即可得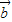 的坐标,然后求出向量的模.
的坐标,然后求出向量的模.
解答:解:根据题意,若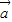 ∥
∥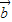 ,,则有-1×1=(m+2)×m,
,,则有-1×1=(m+2)×m,
解可得m=-1,
则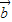 =(-1,-1),
=(-1,-1),
则|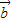 |=
|=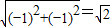
故选A.
点评:本题考查向量平行的坐标表示与向量的坐标计算,关键是求出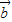 的坐标.
的坐标.
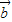 的坐标,然后求出向量的模.
的坐标,然后求出向量的模.解答:解:根据题意,若
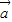 ∥
∥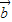 ,,则有-1×1=(m+2)×m,
,,则有-1×1=(m+2)×m,解可得m=-1,
则
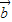 =(-1,-1),
=(-1,-1),则|
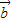 |=
|=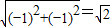
故选A.
点评:本题考查向量平行的坐标表示与向量的坐标计算,关键是求出
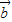 的坐标.
的坐标. 
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知向量
=(1,-m),
=(m2,m),则向量
+
所在的直线可能为( )
| a |
| b |
| a |
| b |
| A、x轴 |
| B、第一、三象限的角平分线 |
| C、y轴 |
| D、第二、四象限的角平分线 |
已知向量
=(1,m),
=(2,n),
=(3,t),且
∥
,
⊥
,则|
|2+|
|2的最小值为( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、20 | B、16 | C、10 | D、4 |