Question

【题目】如图，已知函数，点、分别是的图象与轴、轴的交点，、分别是的图象上横坐标为、的两点，轴，且、、三点共线．

（1）求函数的解析式；

（2）若，，求；

（3）若关于的函数在区间上恰好有一个零点，求实数的取值范围．

Answer 1

【答案】（1）；（2）；（3）．

【解析】

（1）求出点的横坐标，线段中点坐标，再求函数的最小正周期，从而求出、的值，即可写出函数解析式；

（2）由题意得出，再利用诱导公式可求出的值；

（3）由函数的解析式，利用分离常数法得出，求出时，的范围，可得出关于的不等式，解出即可.

（1）根据题意，点与点关于点对称，点的横坐标为.

又点与点关于直线对称，

函数的最小正周期，，

又，，

解得，，，因此，；

（2）由，，，

所以，，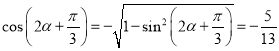

所以；

（3），

令，得，

当时，，所以，

所以，解得，

所以实数的取值范围是.