题目内容
在几何体ABCDE中,AB=AD=BC=CD=2,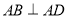 ,且
,且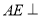 平面
平面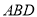 ,平面
,平面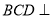 平面
平面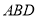 .
.
(1)当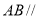 平面
平面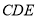 时,求
时,求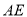 的长;
的长;
(2)当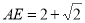 时,求二面角
时,求二面角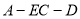 的大小.
的大小.
(1) ;(2)
;(2)
【解析】
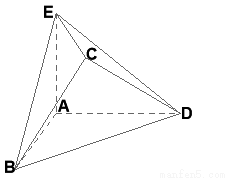
试题分析:(1)设AE=a,如图建立空间直角坐标系,则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),取BD中点T,连CT,AT,求出平面CDE的一个法向量为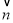 ,根据AB||平面CDE可得
,根据AB||平面CDE可得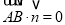 由此可求出a值,即AE长;(2)转化为求两平面法向量的夹角,由(1)易知平面CDE的一个法向量
由此可求出a值,即AE长;(2)转化为求两平面法向量的夹角,由(1)易知平面CDE的一个法向量 ,可证平面AEC的一个法向量
,可证平面AEC的一个法向量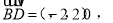 利用向量夹角公式即可求得,注意二面角与向量夹角的关系;
利用向量夹角公式即可求得,注意二面角与向量夹角的关系;
试题解析:(1)设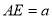 ,如图,建立空间直角坐标系,
,如图,建立空间直角坐标系,
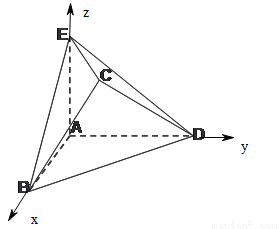
则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),
取BD的中点T,连接CT,AT,则CT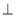 BD.
BD.
又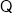 平面BCD
平面BCD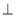 平面ABD,
平面ABD,
所以CT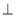 平面BCD,
平面BCD,
所以CT//AE.
 AB=AD=BC=CD=2,
AB=AD=BC=CD=2, ,
,
所以CD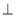 CB,
CB,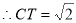 ,
,
 C(1,1,
C(1,1, ),
),

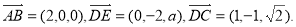
设平面CDE的法向量为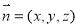 ,
,
则有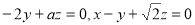 ,
, 
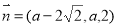 .
.
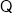 AB//平面CDE,
AB//平面CDE,

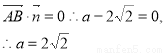
即AE的长为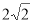 .
.
(2)连接AC,当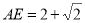 时,由(1)可知平面CDE的一个法向量
时,由(1)可知平面CDE的一个法向量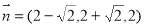 ,
,
又BD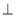 AT,BD
AT,BD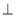 AE,
AE, BD
BD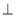 平面ACE,
平面ACE,
 平面ACE的一个法向量
平面ACE的一个法向量

 二面角
二面角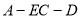 的大小为
的大小为 .
.
考点:二面角及其求法,空间向量求平面夹角

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,则目标函数
,则目标函数 的最小值为 .
的最小值为 . 中,
中, ,
, ,则数列
,则数列 的通项公式为 .
的通项公式为 .
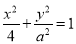 和双曲线
和双曲线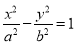 有共同的焦点,连接椭圆的焦点和短轴的一个端点所得直线和双曲线的一条渐近线平行,设双曲线的离心率为
有共同的焦点,连接椭圆的焦点和短轴的一个端点所得直线和双曲线的一条渐近线平行,设双曲线的离心率为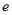 ,则
,则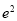 等于( )
等于( ) B.
B.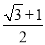
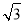 D.
D.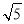
 名学生负责校内
名学生负责校内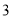 个不同地段的卫生工作,每个地段至少有
个不同地段的卫生工作,每个地段至少有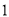 名学生的分配方案共有( )
名学生的分配方案共有( )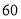 种 B.
种 B.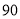 种 C.
种 C.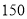 种 D.
种 D. 种
种 是椭圆
是椭圆 的左焦点,O为坐标原点,点P在椭圆上,则
的左焦点,O为坐标原点,点P在椭圆上,则 的最大值为.
的最大值为.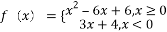 ,若互不相等的实数
,若互不相等的实数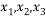 满足
满足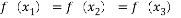 ,则
,则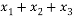 的取值范围是( )
的取值范围是( )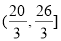 B.
B.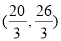 C.
C. D.
D.
 的圆心
的圆心 到抛物线
到抛物线 的准线
的准线 的距离为 .
的距离为 . 上随机选取一个数X,则
上随机选取一个数X,则 的概率等于__________.
的概率等于__________.