题目内容
在△ABC中，若A：B：C=1：2：3，则a：b：c= ．
考点：正弦定理
专题：解三角形
分析：由三角形的内角和以及三个角的比例关系，求出三个角，利用正弦定理即可求出比值．
解答：
解：∵A：B：C=1：2：3，A+B+C=180°
∴A=30°，B=60°，C=90°，
∴由正弦定理
=
=
，
得：
=
=
．
∴a：b：c=1：
：2
故答案为：1：
：2．
∴A=30°，B=60°，C=90°，
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
得：
| a | ||
|
| b | ||||
|
| c |
| 1 |
∴a：b：c=1：
| 3 |
故答案为：1：
| 3 |
点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
设非空集合A⊆{1，2，3，4，5}，且若a∈A，则6-a∈A，这样的集合共有（ ）个．
| A、5 | B、6 | C、7 | D、8 |
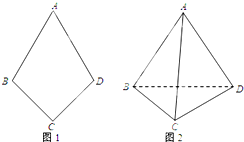如图1，平面四边形ABCD关于直线AC对称，∠A=60°，∠C=
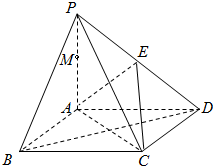如图，棱锥P-ABCD的底面ABCD是矩形，PA⊥面ABCD，PA=AD=4，BD=4