题目内容
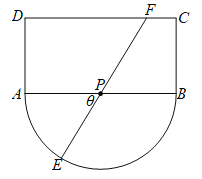
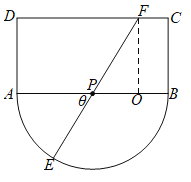
【题目】如城某观光区的平面示意图如图所示,其中矩形![]() 的长
的长![]() 千米,宽
千米,宽![]() 千米,半圆的圆心
千米,半圆的圆心![]() 为
为![]() 中点.为了便于游客观光休闲,在观光区铺设一条由圆弧
中点.为了便于游客观光休闲,在观光区铺设一条由圆弧![]() 、线段
、线段![]() 、
、![]() 组成的观光道路.其中线段
组成的观光道路.其中线段![]() 经过圆心
经过圆心![]() ,且点
,且点![]() 在线段
在线段![]() 上(不含线段端点
上(不含线段端点![]() 、
、![]() ).已知道路
).已知道路![]() 、
、![]() 的造价为
的造价为![]() 元每千米,道路
元每千米,道路![]() 造价为
造价为![]() 元每千米,设
元每千米,设![]() ,观光道路的总造价为
,观光道路的总造价为![]() .
.
(1)试求![]() 与
与![]() 的函数关系式:
的函数关系式:![]() ;
;
(2)当![]() 为何值时,观光道路的总造价
为何值时,观光道路的总造价![]() 最小.
最小.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可知![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,求出
,求出![]() 、
、![]() ,即可求出
,即可求出![]() 与
与![]() 的函数关系式
的函数关系式![]() ;
;
(2)求导数,确定函数的单调性,即可得出当![]() 为何值时,观光道路的总造价
为何值时,观光道路的总造价![]() 最小.
最小.
(1)由题意可知![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,
则![]() ,
,![]() ,
,
![]() ;
;
(2)![]()
令![]() ,即
,即![]() ,解得
,解得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 极大值 |
|
所以,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
因此,当![]() 时,观光道路的总造价最小.
时,观光道路的总造价最小.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到下图的率分布直方图.(同一组数据用该区间的中点值作代表)
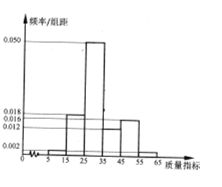
(1)该企业为提高产品质量,开展了质量提升月”活动,活动后再抽样检测,产品三等品数Y近似满足Y~H(10,15,100),请测算“质量提升月”活动后这种产品的“二等品率“(一、二等品其占全部产品百分比)较活动前提高多少个百分点?
(2)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名联客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.
【题目】在某区“创文明城区”(简称“创城”)活动中,教委对本区![]() 四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
(注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值)假设每名高中学生是否参与”创城”活动是相互独立的.
(1)若该区共2000名高中学生,估计![]() 学校参与“创城”活动的人数;
学校参与“创城”活动的人数;
(2)在随机抽查的100名高中学生中,随机抽取1名学生,求恰好该生没有参与“创城”活动的概率;
(3)在上表中从![]() 两校没有参与“创城”活动的同学中随机抽取2人,求恰好
两校没有参与“创城”活动的同学中随机抽取2人,求恰好![]() 两校各有1人没有参与“创城”活动的概率是多少?
两校各有1人没有参与“创城”活动的概率是多少?