题目内容
16.若max{a,b}表示a,b两数中的最大值,若f(x)=max{e|x|,e|x-t|}关于x=2015对称,则t=4030.分析 利用函数y=e|x|的图象和函数y=e|x-t|的图象关于直线x=$\frac{0+t}{2}$对称,从而得出结论.
解答 解:若f(x)=max{e|x|,e|x-t|}关于x=2015对称,
由函数y=e|x|的图象关于x=0对称,函数y=e|x-t|的图象关于x=t对称,
即有函数f(x)的图象关于x=$\frac{0+t}{2}$对称,
即有$\frac{t}{2}$=2015,求得t=4030,
故答案为:4030.
点评 本题主要考查指数函数的单调性,分段函数的应用,考查函数的对称性,属于基础题.

练习册系列答案
相关题目
7.若集合A={x|-2<x<1},B={x|0<x<2},则集合A∩B=( )
| A. | { x|-1<x<1} | B. | { x|-2<x<1} | C. | { x|-2<x<2} | D. | { x|0<x<1} |
4.已知sinα=$\frac{4}{5}$,$\frac{π}{2}$<α<π,那么tanα的值是( )
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
8.$\int_1^2{(x-\frac{1}{x})}dx$的值是( )
| A. | 0 | B. | 1.5-ln2 | C. | 3-ln2 | D. | 1 |
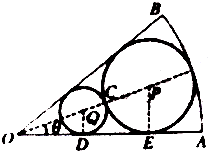 如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.
如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.