题目内容

1．已知函数f（x）=$\left\{\begin{array}{l}{x+1，x≤0}\\{{x}^{2}-2x+1，x＞0}\end{array}\right.$，若关于x的方程f2（x）-af（x）=0恰有5个不同的实数解，则a的取值范围是（0，1）．

分析 作f（x）的图象，从而由f2（x）-af（x）=f（x）（f（x）-a）=0可得f（x）=a有三个不同的解，从而结合图象解得．

解答 解：作f（x）的图象如下，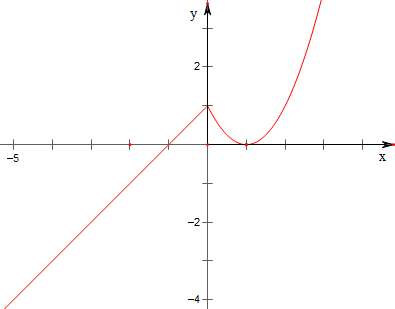
，
f2（x）-af（x）=f（x）（f（x）-a）=0，
∴f（x）=0或f（x）=a；
∵f（x）=0有两个不同的解，
故f（x）=a有三个不同的解，
故a∈（0，1）；
故答案为：（0，1）．

点评 本题考查了函数的零点与方程的根的关系应用．

练习册系列答案
相关题目
11．如图所示平行四边形AOBD中，设向量$\overrightarrow{OA}$=a，$\overrightarrow{OB}$=b又$\overrightarrow{BM}$=$\frac{1}{3}$$\overrightarrow{BC}$，$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{CD}$，用a，b表示$\overrightarrow{OM}$、$\overrightarrow{ON}$、$\overrightarrow{MN}$．
12．下列结论正确的个数是（　　）
①已知复数z=i（1-i），z在复平面内对应的点位于第四象限；
②不等式x-2y+6＞0表示的平面区域是直线x-2y+6=0的右下方；
③命题p：“?x0∈R，x${\;}_{0}^{2}$-x0-1＞0”的否定?p：“?x∈R，x2-x-1≤0”．
A．3B．2C．1D．0
9．函数f（x）=lnx+2x-6的零点在区间（a，a+1），a∈Z内，则a=2．
16．PM2.5是指环境空气中空气动力学当量直径小于或等于2.5 微米的颗粒物．一般情况下PM2.5浓度越高，就代表空气污染越严重，如图所示的茎叶图表示的是某市区甲、乙两个监测站某10日内每天的PM2.5浓度读数（单位：μg/m3），则下列说法正确的是（　　）
A．这10 日内甲、乙监测站读数的极差相等
B．这10 日内甲、乙监测站读数的中位数中，乙的较大
C．这10 日内乙监测站读数的众数与中位数相等
D．这10 日内甲、乙监测站读数的平均数相等
6．已知函数f（x）=alnx+$\frac{1}{2}$x2，a∈R．
（1）若a=-1时，讨论函数f（x）的单调性．
（2）当x≥1时，f（x）＞lnx恒成立，求a的取值．
13．下列运算正确的是（　　）
A．a2•a3=a6B．a8÷a4=a2C．（-ab）2=ab2D．a3+a3=2a3
10．已知双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左，右焦点分别为F1，F2，在双曲线的右支存在一点P，使PF1=3PF2，求点P的坐标．
11．已知点C的坐标为（-1，2），O位原点．
（1）直线l不过原点且在x轴、y轴上截距相等，点C（-1，2）到直线l的距离为2，求直线l的方程；
（2）已知点P（x0，y0），直线CM⊥MP，且|CM|=2，若|PM|=|PO|，求使|PM|取最小值时P点坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网