题目内容
9.下列函数中,在区间(-∞,0)上是减函数的是( )| A. | y=x2 | B. | y=2x | C. | y=x3 | D. | y=lgx |
分析 根据二次函数、指数函数及y=x3的单调性,以及对数函数的定义域便可判断每个选项的正误,从而找出正确选项.
解答 解:y=x2在(-∞,0)上是减函数,y=2x和y=x3在(-∞,0)上都是增函数,y=lgx在(-∞,0)上不存在;
∴在区间(-∞,0)上是减函数的是A.
故选:A.
点评 考查二次函数,指数函数和y=x3的单调性,要熟悉y=x3的图象,以及对数函数的定义域.

练习册系列答案
相关题目
19.为了解某地脐橙种植情况,调研小组在该地某脐橙种植园中随机抽出30棵,每棵挂果情况如下(单位:个):
157 161 170 180 181 172 162 157 191 182 181 173 174 165 158
164 159 159 168 169 176 178 158 169 176 187 184 175 169 175
(1)完成频数分布表,并作出频率分布直方图.
(2)如果挂果在175个以上(包括175)定义为“高产”,挂果在175个以下(不包括175)定义为“非高产”.用分层抽样的方法从“高产”和“非高产”中抽取5棵,再从这5棵中选2棵,那么至少有一棵是“高产”的概率是多少?
157 161 170 180 181 172 162 157 191 182 181 173 174 165 158

164 159 159 168 169 176 178 158 169 176 187 184 175 169 175
(1)完成频数分布表,并作出频率分布直方图.
| 挂果个数区间 | [155,165) | [165,175) | [175,185) | [185,195] |
| 频数 |
14.已知集合A={x|y=lg(5-x)},B={y|y=lg(5-x)},则A∩B=( )
| A. | ∅? | B. | R | C. | (-∞,5) | D. | [0,5] |
18.若函数f(x)=$\left\{\begin{array}{l}{{5}^{-x},x∈(-1,0]}\\{{5}^{x},x∈[0,1]}\end{array}\right.$,则f(log54)=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{4}$ | D. | 4 |
19.化简$\frac{sin(2π-α)tan(π+α)sin(\frac{π}{2}+α)}{cos(π-α)tan(3π-α)}$=( )
| A. | cosα | B. | -sinα | C. | -cosα | D. | sinα |
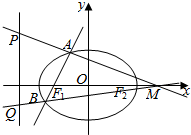 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.