题目内容
若椭圆ax2+by2=1与直线x+y=1交于点A,B,点M为AB的中点,直线OM(O为原点)的斜率为
,又OA⊥OB,求a,b.
| 2 |
分析:联立直线方程和椭圆方程,利用根与系数关系求出点M的坐标,由直线OM的斜率为
得到关于a,b的一个方程,再由OA⊥OB,即
•
=0得到关于a,b的另一方程,联立求解a,b后验证满足△>0即可.
| 2 |
| OA |
| OB |
解答:解:由
消去y,得(a+b)x2-2bx+b-1=0.
当△=4b2-4(a+b)(b-1)=4(a+b-ab)>0时,
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
.
弦AB的中点坐标为(
,
).
∴OM所在直线斜率
=
①
∵OA⊥OB,即
•
=x1x2+y1y2=x1x2+(1-x1)(1-x2)
=2x1x2-(x1+x2)+1=
-
+1=1-
=0.
得:a+b=1 ②
由①②得:a=2
-2,b=4-2
.
满足不等式△=4b2-4(a+b)(b-1)=4(a+b-ab)>0.
∴a=2
-2,b=4-2
.
|
当△=4b2-4(a+b)(b-1)=4(a+b-ab)>0时,
设A(x1,y1),B(x2,y2),则x1+x2=
| 2b |
| a+b |
| b-1 |
| a+b |
弦AB的中点坐标为(
| b |
| a+b |
| a |
| a+b |
∴OM所在直线斜率
| a |
| b |
| 2 |
∵OA⊥OB,即
| OA |
| OB |
=2x1x2-(x1+x2)+1=
| 2(b-1) |
| a+b |
| 2b |
| a+b |
| 2 |
| a+b |
得:a+b=1 ②
由①②得:a=2
| 2 |
| 2 |
满足不等式△=4b2-4(a+b)(b-1)=4(a+b-ab)>0.
∴a=2
| 2 |
| 2 |
点评:本题考查了直线与圆锥曲线的关系,考查了数量积判断两个向量的垂直关系,涉及直线与圆锥曲线的关系问题,常采用“设而不求”的解题思想方法,该题是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
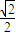 ,且OA⊥OB,求椭圆的方程.
,且OA⊥OB,求椭圆的方程.