题目内容
若椭圆ax2+by2=1与直线x+y=1交于A、B两点，M为AB的中点，直线OM（O为原点）的斜率为
| ||
| 2 |
分析：欲求椭圆方程，需求a、b，为此需要得到关于a、b的两个方程，由OM的斜率为
．OA⊥OB，易得a、b的两个方程．
| ||
| 2 |
解答：解：设A（x1，y1），B（x2，y2），M（
，
）．
∴（a+b）x2-2bx+b-1=0．
由x+y=1，ax2+by2=1，
∴
=
，
=1-
=
．
∴M（
，
）．
∵kOM=
，∴b=
a．①
∵OA⊥OB，∴
•
=-1．
∴x1x2+y1y2=0．
∵x1x2=
，y1y2=（1-x1）（1-x2），
∴y1y2=1-（x1+x2）+x1x2
=1-
+
=
．
∴
+
=0．
∴a+b=2．②
由①②得a=2（
-1），b=2
（
-1）．
∴所求方程为2（
-1）x2+2
（
-1）y2=1．
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∴（a+b）x2-2bx+b-1=0．
由x+y=1，ax2+by2=1，
∴
| x1+x2 |
| 2 |
| b |
| a+b |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| a |
| a+b |
∴M（
| b |
| a+b |
| a |
| a+b |
∵kOM=
| ||
| 2 |
| 2 |
∵OA⊥OB，∴
| y1 |
| x1 |
| y2 |
| x2 |
∴x1x2+y1y2=0．
∵x1x2=
| b-1 |
| a+b |
∴y1y2=1-（x1+x2）+x1x2
=1-
| 2b |
| a+b |
| b-1 |
| a+b |
| a-1 |
| a+b |
∴
| b-1 |
| a+b |
| a-1 |
| a+b |
∴a+b=2．②
由①②得a=2（
| 2 |
| 2 |
| 2 |
∴所求方程为2（
| 2 |
| 2 |
| 2 |
点评：本题主要考查了椭圆的应用，直线与圆锥曲线的位置关系的问题．一般是把直线与圆锥曲线的方程联立，充分利用判别式和韦达定理求得问题的解决．
练习册系列答案
相关题目
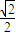，且OA⊥OB，求椭圆的方程．