题目内容
若椭圆ax2+by2=1与直线x+y=1交于A、B两点,且|AB|=2
,又M为AB的中点,若O为坐标原点,直线OM的斜率为
,求该椭圆的方程.
| 2 |
| ||
| 2 |
分析:设A(x1,y1),B(x2,y2),AB的中点M(x0,y0).联立
,化为(a+b)x2-2bx+b-1=0,
利用根与系数的关系和中点坐标公式可得OM的斜率=
=
,再利用弦长公式可得2
=|AB|=
,联立解得即可.
|
利用根与系数的关系和中点坐标公式可得OM的斜率=
| y0 |
| x0 |
| ||
| 2 |
| 2 |
| (1+1)[(x1+x2)2-4x1x2] |
解答:解:设A(x1,y1),B(x2,y2),AB的中点M(x0,y0).
联立
,化为(a+b)x2-2bx+b-1=0,
∵直线与椭圆相交于不同的两点,
∴△=4b2-4(a+b)(b-1)>0,(*)
∴x1+x2=
,x1x2=
.
∴x0=
=
,
y0=1-x0=1-
=
.
∴OM的斜率=
=
=
,即b=
a.
又2
=|AB|=
=
,
化为(a+b)2=a+b-ab,
联立
,
解得
,满足(*)
∴该椭圆的方程为:
+
=1.
联立
|
∵直线与椭圆相交于不同的两点,
∴△=4b2-4(a+b)(b-1)>0,(*)
∴x1+x2=
| 2b |
| a+b |
| b-1 |
| a+b |
∴x0=
| x1+x2 |
| 2 |
| b |
| a+b |
y0=1-x0=1-
| b |
| a+b |
| a |
| a+b |
∴OM的斜率=
| y0 |
| x0 |
| a |
| b |
| ||
| 2 |
| 2 |
又2
| 2 |
| (1+1)[(x1+x2)2-4x1x2] |
2[(
|
化为(a+b)2=a+b-ab,
联立
|
解得
|
∴该椭圆的方程为:
| x2 |
| 3 |
| ||
| 3 |
点评:不同考查了直线与椭圆相交问题转化为方程联立得到根与系数的关系、中点坐标三个、弦长公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
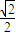 ,且OA⊥OB,求椭圆的方程.
,且OA⊥OB,求椭圆的方程.