题目内容
3.已知定义在R上的函数f(x)满足f(x+1)=-f(x),且f(x)=$\left\{\begin{array}{l}{1,-1<x≤0}\\{-1,0<x≤1}\end{array}\right.$,则下列函数值为1的是( )| A. | f(2.5) | B. | f(f(2.5)) | C. | f(f(1.5)) | D. | f(2) |
分析 由f(x+1)=-f(x),得到函数的周期是2,根据分段函数的表达式结合函数的周期性进行求解即可.
解答 解:由f(x+1)=-f(x),得f(x+2)=-f(x+1)=f(x),
则函数的周期是2,
则f(2.5)=f(2+0.5)=f(0.5)=-1,
f(f(2.5))=f(-1)=f(-1+2)=f(1)=-1
f(f(1.5))=f(f(2-0.5))=f(f(-0.5))=f(1)=-1,
f(2)=f(0)=1,
即列函数值为1的f(2),
故选:D.
点评 本题主要考查函数值的计算,根据函数的周期性结婚分段函数的表达式利用代入法和转化法是解决本题的关键.

练习册系列答案
相关题目
14.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x,x≤0}\\{xlnx,x>0}\end{array}\right.$ 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
| A. | (1,2) | B. | (-1,0) | C. | (-2,-1) | D. | (-6,-1) |
11.过点A(3,1)的直线l与圆C:x2+y2-4y-1=0相切于点B,则$\overrightarrow{CA}•\overrightarrow{CB}$=( )
| A. | 0 | B. | $\sqrt{5}$ | C. | 5 | D. | $\frac{{\sqrt{50}}}{3}$ |
8.复数Z=$\frac{2+ai}{1+i}$(a∈R)在复平面内对应的点在虚轴上,则a=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
15.若复数$\frac{a-3i}{1-2i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| A. | -2 | B. | 4 | C. | -6 | D. | 6 |
12.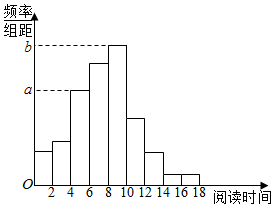 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:| 编号 | 分组 | 频数 |
| 1 | [0,2) | 12 |
| 2 | [2,4) | 16 |
| 3 | [4,6) | 34 |
| 4 | [6,8) | 44 |
| 5 | [8,10) | 50 |
| 6 | [10,12) | 24 |
| 7 | [12,14) | 12 |
| 8 | [14,16) | 4 |
| 9 | [16,18) | 4 |
| 合计 | 200 | |
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
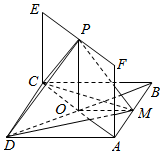 如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1.
如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1.