题目内容
函数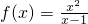
- A.在(0,2)上单调递减
- B.在(-∞,0)和(2,+∞)上单调递增
- C.在(0,2)上单调递增
- D.在(-∞,0)和(2,+∞)上单调递减
B
分析:先求函数的定义域,再求函数的导数,令导数大于0,在定义域成立的前提下,解得的x的范围是函数的增区间,令导数小于0,在定义域成立的前提下,解得的x的范围为函数的减区间.
解答:函数的定义域为{x|x≠1}
函数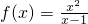 的导数为
的导数为 ,令导数大于0,即
,令导数大于0,即 >0,解得x<0,或x>2
>0,解得x<0,或x>2
令导数小于0,即 <0,解得0<x<2,又∵
<0,解得0<x<2,又∵
∴函数的增区间为(-∞,0)和(2,+∞),减区间为(0,1)和(1,2)
故选B
点评:本题主要考查了利用导数判断函数的单调性,一定注意单调区间是定义域的子区间,必须在定义域成立的前提下求单调区间.
分析:先求函数的定义域,再求函数的导数,令导数大于0,在定义域成立的前提下,解得的x的范围是函数的增区间,令导数小于0,在定义域成立的前提下,解得的x的范围为函数的减区间.
解答:函数的定义域为{x|x≠1}
函数
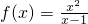 的导数为
的导数为 ,令导数大于0,即
,令导数大于0,即 >0,解得x<0,或x>2
>0,解得x<0,或x>2令导数小于0,即
 <0,解得0<x<2,又∵
<0,解得0<x<2,又∵∴函数的增区间为(-∞,0)和(2,+∞),减区间为(0,1)和(1,2)
故选B
点评:本题主要考查了利用导数判断函数的单调性,一定注意单调区间是定义域的子区间,必须在定义域成立的前提下求单调区间.

练习册系列答案
相关题目