题目内容
若方程 在
在 上有解,则实数
上有解,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. ∪ ∪ |
A
解析试题分析:方程 在
在 上有解,等价于
上有解,等价于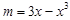 在
在 上有解,故
上有解,故 的取值范围即为函数
的取值范围即为函数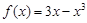 在
在 上的值域,求导可得
上的值域,求导可得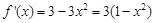 ,令
,令 可知
可知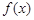 在
在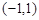 上单调递增,在
上单调递增,在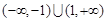 上单调递减,故当
上单调递减,故当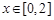 时
时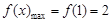 ,
,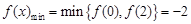 ,故
,故 的取值范围
的取值范围 .
.
考点:1、函数单调性,值域;2、导数.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
已知指数函数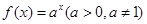 ,且过点(2,4),
,且过点(2,4), 的反函数记为
的反函数记为 ,则
,则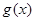 的解析式是:( )
的解析式是:( )
A. | B. | C. | D. |
已知函数 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )
A. | B.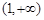 | C. | D.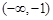 |
设 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. | C. | D. |
设函数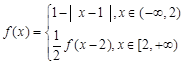 ,则函数
,则函数 的零点的个数为( )
的零点的个数为( )
| A.4 | B.7 | C.6 | D.无穷多个 |
已知函数 (
( ),若函数
),若函数 在
在 上有两个零点,则
上有两个零点,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 ,则
,则 ( )
( )
| A.2014 | B. | C.2015 | D. |
函数y=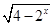 的值域是( )
的值域是( )
| A.[0,+∞) | B.[0,2] |
| C.[0,2) | D.(0,2) |
 的图像大致为( )
的图像大致为( )