题目内容
设 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. | C. | D. |
D
解析试题分析:构造函数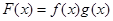 ,因为当
,因为当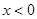 时,
时, 即
即 ,所以函数
,所以函数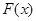 在
在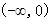 单调递增,又
单调递增,又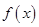 、
、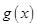 分别是定义在
分别是定义在 上的奇函数和偶函数,所以
上的奇函数和偶函数,所以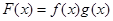 为奇函数,从而
为奇函数,从而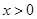 时
时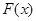 为增函数且
为增函数且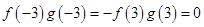 ,故不等式
,故不等式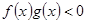 的解集为
的解集为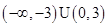 ,故选D.
,故选D.
考点:1.函数的奇偶性;2.导数在单调性上的应用;3.函数的图像.

练习册系列答案
相关题目
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C.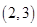 | D. |
已知函数 ,若存在实数
,若存在实数 满足
满足 ,且
,且 ,则
,则 的取值范围( )
的取值范围( )
| A.(20,32) | B.(9,21) | C.(8,24) | D.(15,25) |
下列函数中,既是偶函数,又在区间 内是增函数的为( )
内是增函数的为( )
A. | B. |
C. | D. |
已知 ,
, ,规定:当
,规定:当 时,
时,  ;当
;当 时,
时, ,则
,则 ( )
( )
A.有最小值 ,最大值1 ,最大值1 | B.有最大值1,无最小值 |
C.有最小值 ,无最大值 ,无最大值 | D.有最大值 ,无最小值 ,无最小值 |
若方程 在
在 上有解,则实数
上有解,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. ∪ ∪ |
定义在R上的奇函数 满足
满足 ,且在
,且在 上是增函数,则有( )
上是增函数,则有( )
A.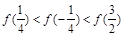 | B. |
C. | D. |
由表格中的数据可以判定方程 的一个零点所在的区间是
的一个零点所在的区间是 ,则
,则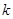 的值为( )
的值为( )
 | -1 | 0 | 1 | 2 | 3 |
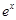 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
 | 1 | 2 | 3 | 4 | 5 |
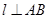 于E,当
于E,当 从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设
从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设 ,左侧部分面积为
,左侧部分面积为 ,则
,则 的图像大致为( )
的图像大致为( )
