题目内容
已知函数 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )
A. | B.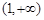 | C. | D.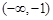 |
B
解析试题分析:
∵ =
= =
= =
= ,故
,故 是偶函数,当
是偶函数,当 ≥0时,
≥0时, =
= 是增函数,故
是增函数,故 ≥
≥ =1,由偶函数图像关于
=1,由偶函数图像关于 轴对称知,
轴对称知, 在(-∞,0)是减函数,值域为(1,+∞),作出函数
在(-∞,0)是减函数,值域为(1,+∞),作出函数 与y=k,由图可知,当关于
与y=k,由图可知,当关于 的方程
的方程 有两个不同的实根时,则实数
有两个不同的实根时,则实数 的取值范围是
的取值范围是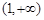 ,故选B.
,故选B.
考点:1.函数的奇偶性、单调性、值域;2.数形结合思想.

练习册系列答案
相关题目
 是定义在
是定义在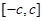 上的奇函数,其图象如图所示,令
上的奇函数,其图象如图所示,令 ,则下列关于函数
,则下列关于函数 的叙述正确的是()
的叙述正确的是()
A.若 ,则函数 ,则函数 的图象关于原点对称 的图象关于原点对称 |
B.若 ,则方程 ,则方程 有大于2的实根 有大于2的实根 |
C.若 ,则方程 ,则方程 有两个实根 有两个实根 |
D.若 ,则方程 ,则方程 有两个实根 有两个实根 |
下列函数是偶函数,且在 上单调递增的是( )
上单调递增的是( )
A. | B. | C. | D. |
下列函数中,既是偶函数,又在区间 内是增函数的为( )
内是增函数的为( )
A. | B. |
C. | D. |
函数 的零点是( )
的零点是( )
A. | B. | C. | D. |
若方程 在
在 上有解,则实数
上有解,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. ∪ ∪ |
设 是定义在R上的奇函数,当
是定义在R上的奇函数,当 ,则
,则 = ( )
= ( )
| A.—3 | B.—1 | C.1 | D.3 |
函数 是奇函数的充要条件是
是奇函数的充要条件是
A. | B. | C. | D. |
 使关于t的二次方程
使关于t的二次方程 的根都是绝对值不超过1的实数,那么这样的点
的根都是绝对值不超过1的实数,那么这样的点 的集合在平面内的区域的形状是( )
的集合在平面内的区域的形状是( )