题目内容
点M(5,3)到抛物线x2=ay(a>0)的准线的距离为6,那么抛物线的方程是 .
【答案】分析:先根据抛物线的方程表示出抛物线的准线方程,然后表示出点M到准线的距离,根据结果为6求得a,则抛物线的方程可得.
解答:解:根据抛物线方程可知抛物线的准线为y=-
则点M到准线的距离为|3+ |=6,求得a=12或a=-36,
|=6,求得a=12或a=-36,
故抛物线方程为x2=12y或x2=-36y,
故答案为:x2=12y或x2=-36y.
点评:本题主要考查了抛物线的标准方程.考查了学生对抛物线的基础知识和标准方程的理解和运用.
解答:解:根据抛物线方程可知抛物线的准线为y=-

则点M到准线的距离为|3+
 |=6,求得a=12或a=-36,
|=6,求得a=12或a=-36,故抛物线方程为x2=12y或x2=-36y,
故答案为:x2=12y或x2=-36y.
点评:本题主要考查了抛物线的标准方程.考查了学生对抛物线的基础知识和标准方程的理解和运用.

练习册系列答案
相关题目
点M(5,3)到抛物线y=ax2的准线的距离为6,那么抛物线的方程是( )
| A、y=12x2 | ||||
| B、y=-36x2 | ||||
| C、y=12x2或y=-36x2 | ||||
D、y=
|
 x2或y=-
x2或y=-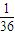 x2
x2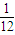 x2或y=-
x2或y=-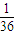 x2
x2