题目内容
已知等差数列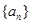 ,
, 则它的公差是( )
则它的公差是( )
| A.1 | B.2 | C.3 | D.4 |
A
解析试题分析:因为等差数列中,结合前n项和的公式可知, ,故选A.
,故选A.
考点:本题主要考查等差数列的通项公式的求解和前n项和的关系的运用。
点评:解决该试题的关键是能利用前15项的和,得到首项与其公差的基本量的关系式,进而求解的大公差的值。

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
若数列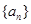 是等差数列,且
是等差数列,且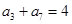 ,则数列
,则数列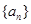 的前
的前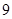 项和
项和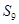 等于
等于
A.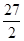 | B.18 | C.27 | D.36 |
等差数列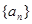 中,已知前
中,已知前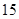 项的和
项的和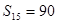 ,则
,则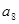 等于( )
等于( )
A.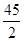 | B.12 | C.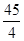 | D.6 |
在数列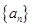 中,
中, ,
,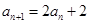 ,则
,则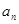 等于( )
等于( )
A.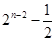 | B.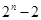 | C.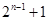 | D.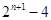 |
已知数列 为等差数列,若
为等差数列,若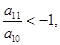 且它们的前
且它们的前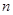 项和
项和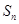 有最大值,则使得
有最大值,则使得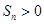 的
的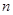 的最大值为( )
的最大值为( )
| A.11 | B.19 | C.20 | D.21 |
已知递增等差数列 中,
中,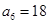 且
且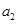 是
是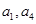 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为
| A.180 | B.198 | C.189 | D.168 |
已知等差数列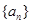 中,前
中,前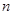 项和
项和 ,且
,且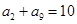 ,则
,则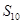 等于( )
等于( )
A.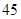 | B.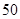 | C.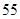 | D.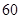 |
已知等差数列{an}的前n项和为Sn,S9=-36,S13=-104,等比数列{bn}中,b5=a5,b7=a7,则b6的值为
A.±4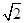 | B.-4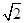 | C.4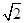 | D.无法确定 |
两等差数列{an}、{bn}的前n项和的比 ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C. | D. |