题目内容
已知f(x)=3mx2-2(m+n)x+n(m≠0)满足f(0)•f(1)>0,设x1,x2是方程f(x)=0的两根,则|x1-x2|的取值范围为
- A.
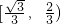
- B.
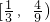
- C.
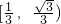
- D.
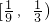
A
分析:由f(0)•f(1)>0可求出m和n的不等关系,x1,x2是方程f(x)=0的两根,由维达定理可表示出x1+x2和x1•x2,而|x1-x2|2=(x1+x2)2-4x1•x2,可表示为m和n的关系式,求范围即可.
解答:由f(0)•f(1)>0可得n(m-n)>0,不等式两边同除以m2,则 -
-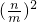 >0,即0<
>0,即0< <1.
<1.
维达定理x1+x2= 和x1•x2=
和x1•x2=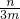 ,
,
所以|x1-x2|2=(x1+x2)2-4x1•x2= =
=
因为0< <1,所以
<1,所以 ≤|x1-x2|2<
≤|x1-x2|2< ,所以
,所以 <|x1-x2|<
<|x1-x2|<
故选A
点评:本题考查二次方程的根和系数的关系、二次函数的范围问题,考查利用所学知识分析问题、解决问题的能力.
分析:由f(0)•f(1)>0可求出m和n的不等关系,x1,x2是方程f(x)=0的两根,由维达定理可表示出x1+x2和x1•x2,而|x1-x2|2=(x1+x2)2-4x1•x2,可表示为m和n的关系式,求范围即可.
解答:由f(0)•f(1)>0可得n(m-n)>0,不等式两边同除以m2,则
 -
-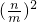 >0,即0<
>0,即0< <1.
<1.维达定理x1+x2=
 和x1•x2=
和x1•x2=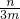 ,
,所以|x1-x2|2=(x1+x2)2-4x1•x2=
 =
=
因为0<
 <1,所以
<1,所以 ≤|x1-x2|2<
≤|x1-x2|2< ,所以
,所以 <|x1-x2|<
<|x1-x2|<
故选A
点评:本题考查二次方程的根和系数的关系、二次函数的范围问题,考查利用所学知识分析问题、解决问题的能力.

练习册系列答案
相关题目