题目内容
若关于x的方程4x-2x+2+4m=0有唯一解,求实数m的取值范围.
解:方法一:令t=2x,原方程化为t2-4t+4m=0, ①
∵原方程有唯一解,
∴关于t的方程①有唯一大于0的解.
令f(t)=t2-4t+4m,考查f(t)的函数图象,如下图.
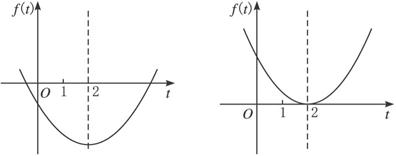
当![]()
即![]() 或16-16m=0时,
或16-16m=0时,
关于t的方程①有唯一的大于0的解.
解得m≤0或m=1.
故m的取值范围是{m|m≤0或m=1}.
方法二:设t=2x,原方程化为t2-4t+4m=0有唯一大于0的解,设为t1>0,另一解t2≤0或t2=t1,则有
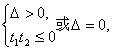
即1![]() 或16-16m=0,
或16-16m=0,
解得m≤0或m=1,
故m的取值范围是{m|m≤0或m=1}.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目