题目内容
3.已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3).(1)若点P(m,m+1)在圆C上,求直线PQ的斜率;
(2)若M是圆C上任一点,求|MQ|的最大值和最小值;
(3)若点N(a,b)满足关系式a2+b2-4a-14b+45=0,求$\frac{b-3}{a+3}$的最大值.
分析 (1)由点P(m,m+1)在圆上,可得m的方程,解方程可得;
(2)由(1)配方可得圆C:(x-2)2+(y-7)2=8,可得$r=2\sqrt{2}$,$|{CQ}|=4\sqrt{2}$,结合图象易得最值;
(3)设$E({-3,3}),k=\frac{b-3}{a+3}$,当过点E的直线与圆相切时,k取最大值,结合点到直线的距离公式可得.
解答 解:(1)∵点P(m,m+1)在圆上,
∴m2+(m+1)2-4m-14(m+1)+45=0
解得m=4,∴P(4,5),
∴kPQ=$\frac{3-5}{-2-4}$=$\frac{1}{3}$;
(2)由(1)配方可得圆C:(x-2)2+(y-7)2=8,
∴$r=2\sqrt{2}$,$|{CQ}|=4\sqrt{2}$,∴${|{MQ}|_{max}}=|{CQ}|+r=6\sqrt{2}$,
${|{MQ}|_{min}}=|{CQ}|-r=2\sqrt{2}$;
(3)设$E({-3,3}),k=\frac{b-3}{a+3}$,
如图,当过点E的直线与圆相切时,k取最大值.
∵切线方程为y-3=k(x+3),即kx-y+3k+3=0
∴$d=\frac{{|{5k-4}|}}{{\sqrt{{k^2}+1}}}=2\sqrt{2}$,∴$k=\frac{{20±2\sqrt{66}}}{17}$,
∴$\frac{b-3}{a+3}$的最大值为$\frac{{20+2\sqrt{66}}}{17}$.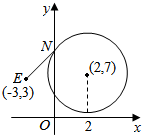
点评 本题考查直线和圆的位置关系,数形结合是解决问题的关键,属中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
14.下列说法中正确的是( )
| A. | 120°角与420°角的终边相同 | |
| B. | 若α是锐角.则2α是第二象限的角 | |
| C. | -240°角与480°角都是第三象限的角 | |
| D. | 60°角与-420°角的终边关于x轴对称 |
15.下列各命题正确的是( )
| A. | 0?{0,1} | B. | 0∈{0,1} | C. | {0}∈{0,1} | D. | 0={0,1} |
19.由不等式组$\left\{\begin{array}{l}{x-y+5≥0}\\{y≥5}\\{0≤x≤2}\end{array}\right.$围成的三角形区域有一个外接圆,在该圆内随机取一点,该点落在三角形内的概率是( )
| A. | $\frac{2}{π}$ | B. | (3-2$\sqrt{2}$)π | C. | $\frac{1}{π}$ | D. | $\frac{1}{2π}$ |
15.设A={x|x为合数},B={x|x为质数},N表示自然数集,若E满足A∪B∪E=N,则这样的集合E( )
| A. | 只有一个 | B. | 只有两个 | C. | 至多3个 | D. | 有无数个 |