题目内容
已知向量 =(sinθ,2),
=(sinθ,2), =(cosθ,1),且
=(cosθ,1),且 ∥
∥ ,其中
,其中 .
.
(1)求sinθ和cosθ的值;
(2)若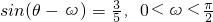 ,求cosω的值.
,求cosω的值.
(1)解:∵向量 =(sinθ,2),
=(sinθ,2), =(cosθ,1),且
=(cosθ,1),且 ∥
∥ ,
,
∴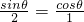 ,即sinθ=2cosθ.
,即sinθ=2cosθ.
∵sin2θ+cos2θ=1, ,
,
解得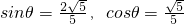 ,
,
∴sin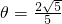 ,cos
,cos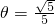 .
.
(2)解:∵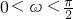 ,
, ,∴
,∴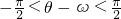 .
.
∵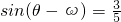 ,
,
∴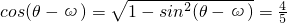 .
.
∴cosω=cos[θ-(θ-ω)]=cosθcos(θ-ω)+sinθsin(θ-ω)= .
.
分析:(1)通过向量的平行,推出sinθ=2cosθ,根据θ的范围,同角三角函数的基本关系式,直接求sinθ和cosθ的值;
(2)根据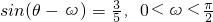 ,
, ,求出
,求出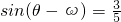 ,结合cosω=cos[θ-(θ-ω)]展开,即可求cosω的值.
,结合cosω=cos[θ-(θ-ω)]展开,即可求cosω的值.
点评:本题考查三角函数的化简求值,向量平行的应用,注意角的范围三角函数的符号,函数值的确定,角的变换的技巧,考查计算能力,常考题型.
 =(sinθ,2),
=(sinθ,2), =(cosθ,1),且
=(cosθ,1),且 ∥
∥ ,
,∴
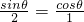 ,即sinθ=2cosθ.
,即sinθ=2cosθ.∵sin2θ+cos2θ=1,
 ,
,解得
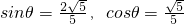 ,
,∴sin
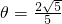 ,cos
,cos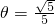 .
.(2)解:∵
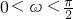 ,
, ,∴
,∴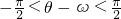 .
.∵
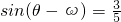 ,
,∴
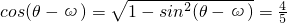 .
.∴cosω=cos[θ-(θ-ω)]=cosθcos(θ-ω)+sinθsin(θ-ω)=
 .
.分析:(1)通过向量的平行,推出sinθ=2cosθ,根据θ的范围,同角三角函数的基本关系式,直接求sinθ和cosθ的值;
(2)根据
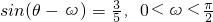 ,
, ,求出
,求出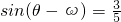 ,结合cosω=cos[θ-(θ-ω)]展开,即可求cosω的值.
,结合cosω=cos[θ-(θ-ω)]展开,即可求cosω的值.点评:本题考查三角函数的化简求值,向量平行的应用,注意角的范围三角函数的符号,函数值的确定,角的变换的技巧,考查计算能力,常考题型.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目