题目内容
已知向量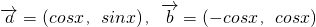 ,
,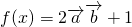 ,设p为“
,设p为“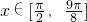 ”q为“|f(x)-m|<3”.若p为q的充分条件,求实数m的取值范围.
”q为“|f(x)-m|<3”.若p为q的充分条件,求实数m的取值范围.
解:∵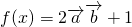 =
= ,
,
p:当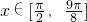 时,
时, ,∴
,∴ ,
,
q:又|f(x)-m|<3,∴m-3<f(x)<m+3,
若p为q的充分条件,则 ,
,
∴ .
.
∴实数m的取值范围是(-2,3- ).
).
分析:利用向量的数量积、三角函数的和差、倍角公式及单调性、充分条件即可得出.
点评:熟练掌握向量的数量积、充分条件、三角函数的和差倍角公式是解题的关键.
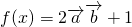 =
= ,
,p:当
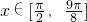 时,
时, ,∴
,∴ ,
,q:又|f(x)-m|<3,∴m-3<f(x)<m+3,
若p为q的充分条件,则
 ,
,∴
 .
.∴实数m的取值范围是(-2,3-
 ).
).分析:利用向量的数量积、三角函数的和差、倍角公式及单调性、充分条件即可得出.
点评:熟练掌握向量的数量积、充分条件、三角函数的和差倍角公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
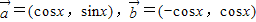 ,
,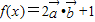 ,设p为“
,设p为“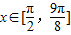 ”q为“|f(x)-m|<3”.若p为q的充分条件,求实数m的取值范围.
”q为“|f(x)-m|<3”.若p为q的充分条件,求实数m的取值范围.