题目内容
设集合 ,对于
,对于 ,记
,记 ,且
,且 ,由所有
,由所有 组成的集合记为:
组成的集合记为: ,
,
(1) 的值为________;
的值为________;
(2)设集合 ,对任意
,对任意 ,
, ,则
,则 的概率为________.
的概率为________.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:由题意知,ai,bi∈M,ai<bi,∵首先考虑M中的二元子集有{1,2},{1,3},…,{5,6},共15个,即为C =15个.
=15个.
又ai<bi,满足 的二元子集有:{1,2},{2,4},{3,6},这时
的二元子集有:{1,2},{2,4},{3,6},这时 ,{1,3},{2,6},这时
,{1,3},{2,6},这时 ,{2,3},{4,6},这时
,{2,3},{4,6},这时 ,共7个二元子集.故集合A中的元素个数为k=15-7+3=11.列举A={
,共7个二元子集.故集合A中的元素个数为k=15-7+3=11.列举A={ ,
, ,
, ,
,
 ,
,
 ,},B={2,3,4,5,6,
,},B={2,3,4,5,6,
 },
}, +
+ =2,
=2,
 +
+ =3,
=3,
 +
+ =2,
=2, +
+ =2,
=2,  +
+ =2,
=2, +
+  =2共6对.∴所求概率为:p=
=2共6对.∴所求概率为:p= .故答案为:11;
.故答案为:11; .
.
考点:古典概型及其概率计算公式.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
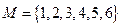 ,对于
,对于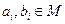 ,记
,记 且
且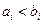 ,由所有
,由所有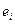 组成的集合设为
组成的集合设为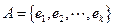 .
.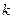 的值;
的值; ,对任意
,对任意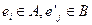 ,试求
,试求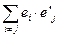 ;
;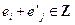 的概率.
的概率. ,对任意
,对任意 ,对任意
,对任意