题目内容
定义运算 则函数
则函数 的图象是
的图象是 
A
解析试题分析:由于题目中给出定义运算 ,那么
,那么 ,结合指数函数的图像可知,分别作图可知选A.
,结合指数函数的图像可知,分别作图可知选A.
考点:本试题主要考查了新定义域的运用,体现了分段函数思想的重要性,一道基础试题。
点评:解决该试题的关键是能理解新定义,得到f(x)的解析式,然后综合运用指数函数的 图像来得到结论。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知函数唯一的零点在区间(1,3),(1,4),(1,5)内,那么下列命题不正确的是
| A.函数f (x)在区间(1,2)或[2,3)内有零点 |
| B.函数f (x)在(3,5)内无零点 |
| C.函数f (x)在(2,5)内一定有零点 |
| D.函数f (x)在(2,4)内不一定有零点 |
函数 的值域是 ( )
的值域是 ( )
A.(- ) ) | B.(- 0) 0)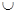 (0,+ (0,+ ) ) |
C.(-1,+ ) ) | D.(- ,-1) ,-1)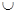 (0,+ (0,+ ) ) |
已知函数 是偶函数,当
是偶函数,当 时,
时, 恒成立,设
恒成立,设 ,则
,则 的大小关系为( )
的大小关系为( )
A. | B.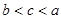 | C. | D. |
下列函数 中,满足对任意
中,满足对任意 ,
,
 (0,
(0, )且
)且 ,都有
,都有 的是 ( )
的是 ( )
A. = = | B. = = | C. = = | D. |
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
 是定义在[-6,6]上的偶函数,且
是定义在[-6,6]上的偶函数,且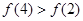 ,则下列各式一定成立的是( )
,则下列各式一定成立的是( )
A.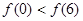 | B.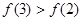 |
C.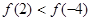 | D.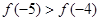 |
设偶函数 的定义域为R,当
的定义域为R,当 时
时 是增函数,则
是增函数,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
下列函数中,既是偶函数又在 单调递增的是( )
单调递增的是( )
A. | B. |
C. | D. |