题目内容
已知函数 是偶函数,当
是偶函数,当 时,
时, 恒成立,设
恒成立,设 ,则
,则 的大小关系为( )
的大小关系为( )
A. | B.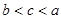 | C. | D. |
A
解析试题分析:因为 时,
时, 恒成立,所以f(x)在
恒成立,所以f(x)在 上是增函数,又因为函数
上是增函数,又因为函数 是偶函数,所以函数f(x)关于直线x=2对称,所以f(x)在
是偶函数,所以函数f(x)关于直线x=2对称,所以f(x)在 上是减函数,因为
上是减函数,因为 ,所以f(6)>f(-1)>f(3),即b<a<c.
,所以f(6)>f(-1)>f(3),即b<a<c.
考点: 抽象函数的单调性与奇偶性,利用其比较数的大小.
点评:由 时,
时, 恒成立, 确定f(x)在
恒成立, 确定f(x)在 上是增函数是解题的关键,然后再根据函数
上是增函数是解题的关键,然后再根据函数 是偶函数,所以函数f(x)关于直线x=2对称,f(x)在
是偶函数,所以函数f(x)关于直线x=2对称,f(x)在 上是减函数,从而转化自变量与对称轴x=2的距离大小的比较问题.
上是减函数,从而转化自变量与对称轴x=2的距离大小的比较问题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知函数 为偶函数,则
为偶函数,则 的值是( )
的值是( )
A. | B. | C. | D. |
函数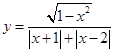 是 ( )
是 ( )
| A.奇函数 | B.偶函数 | C.非奇非偶函数 | D.是奇函数又是偶函数 |
函数  的值域为
的值域为
A. | B. | C. | D. |
下列函数是奇函数的是 ( )
A.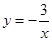 | B. | C. | D. |
函数 在下列哪个区间内有零点
在下列哪个区间内有零点
A.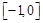 | B. | C. | D. |
定义在 上的函数
上的函数 ,则
,则 的图像与直线
的图像与直线 的交点为
的交点为 、
、 、
、 且
且 ,则下列说法错误的是( )
,则下列说法错误的是( )
A. | B. |
C. | D. |
 的图象可能是 ( )
的图象可能是 ( )
 则函数
则函数 的图象是
的图象是 