题目内容
过不在⊙O上的一点A作直线,交⊙O于B、C两点,且AB·AC=64,OA=10,则⊙O的半径等于 .
思路解析:点A不在⊙O上,有两种情况:(1)点A在⊙O内;(2)点A在⊙O外.
答案:分两种情况讨论:?
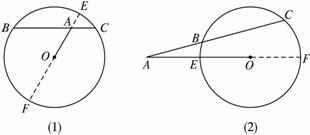
图2-5-5?
(1)当点A在⊙O内部时,如图2-5-5(1)所示.作直线OA交⊙O于E、F,设⊙O的半径为r,
则AE=r-10,AF=r+10.由相交弦定理得(r-10)(r+10)=64.?
解得![]() ,
, ![]() (不合题意,舍去).∴
(不合题意,舍去).∴![]() .?
.?
(2)当点A在⊙O的外部时,延长AO交⊙O于F,设⊙O的半径为R,?
由切割线定理的推论得AB·AC=AE·AF,即64=(10-R)(10+R).
解得R1=6,R2=-6(不合题意,舍去).
∴R=6.?
综上所述,⊙O的半径为![]() 或6.
或6.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: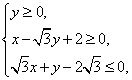 的外接圆C与
的外接圆C与