题目内容
已知可行域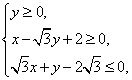 的外接圆C与
的外接圆C与![]() 轴交于点A1、A2,椭圆C1以线段A1A2为短轴,离心率
轴交于点A1、A2,椭圆C1以线段A1A2为短轴,离心率![]()
(Ⅰ)求圆C及椭圆C1的方程;
(Ⅱ)过椭圆C1上一点P(不在坐标轴上)向圆C引两条切线PA、PB、A、B为切点,直线AB分别与x轴、y轴交于点M、N.求△MON面积的最小值.(O为原点).
解析:(Ⅰ)由题意可知,可行域是以![]() 及点
及点![]() 为顶点的三角形,∵
为顶点的三角形,∵![]() ,∴
,∴![]() 为直角三角形, ┅┅┅┅┅┅┅2分
为直角三角形, ┅┅┅┅┅┅┅2分
![]() ∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为
∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为![]() .
.
∵2b=4,∴b=2.又![]() ,可得
,可得![]() .
.
∴所求椭圆C1的方程是![]() . ┅┅┅┅┅┅┅4分
. ┅┅┅┅┅┅┅4分
(Ⅱ)设A(x1,y1),B(x2,y2),![]() ,OA的斜率为
,OA的斜率为![]() ,则PA的斜率为
,则PA的斜率为![]() ,则PA的方程为:
,则PA的方程为:![]() 化简为:
化简为:![]() ,
,
同理PB的方程为![]() ┅┅┅┅┅┅┅6分
┅┅┅┅┅┅┅6分
又PA、PB同时过P点,则x1x0+y1y0=4,x2x0+y2y0=4,
∴AB的直线方程为:x0x+y0y=4 ┅┅┅┅┅┅┅8分
(或者求出以OP为直径的圆,然后求出该圆与圆C的公共弦所在直线方程即为AB的方程)
从而得到![]() 、
、![]() 所以
所以 ![]() ┅┅8分
┅┅8分
![]()
![]()
当且仅当![]() . ┅┅┅┅┅┅┅12分
. ┅┅┅┅┅┅┅12分
(或者利用椭圆的参数方程 、函数求最值等方法求
、函数求最值等方法求![]() 的最大值)
的最大值)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
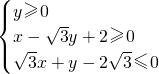 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
. 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明. 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
. 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明. 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
. 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明. 的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率
的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率 .
. 于点Q,判断直线PQ与圆C的位置关系,并给出证明.
于点Q,判断直线PQ与圆C的位置关系,并给出证明.