题目内容
8.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的右焦点为F,点A(3,1),双曲线上取一点P,则2|PA|+|PF|的最小值为4.分析 根据题意,算出双曲线的离心率e=2,右准线为l:x=1.作AN⊥l于N,交双曲线右支于P,连结FP,根据圆锥曲线统一定义得到|PA|+$\frac{1}{2}$|PF|=|PA|+|PN|.由平几知识可得:当A、N、P三点共线时,|PA|+|PN|=|AN|达到最小值,由此即可求出点P的坐标和|PA|+$\frac{1}{2}$|PF|的最小值.
解答 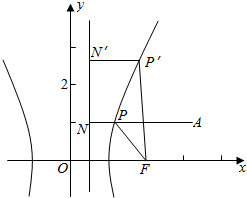 解∵双曲线方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1,
解∵双曲线方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1,
∴a=2,b=2$\sqrt{3}$,c=4,
可得离心率e=2,右准线为l:x=1,
作AN⊥l于N,交双曲线右支于P,连结FP,则
由圆锥曲线统一定义得|PF|=e|PN|=2|PN|,
∴|PN|=$\frac{1}{2}$|PF|,因此,|PA|+$\frac{1}{2}$|PF|=|PA|+|PN|,
当且仅当A、N、P三点共线时,|PA|+|PN|=|AN|达到最小值为|AN|=3-1=2.
∴2|PA|+|PF|的最小值为4.
故答案为:4.
点评 本题着重考查了双曲线的标准方程与简单几何性质、圆锥曲线的统一定义等知识,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
16.已知函数y=lgx的定义域为集合A,集合B={0,1,2},则A∩B=( )
| A. | (0,+∞) | B. | (0,2] | C. | {0,1,2} | D. | {1,2} |
20.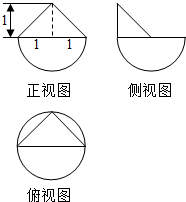 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )
 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 3π+2$\sqrt{2}$-1 | B. | 3π+2$\sqrt{2}$ | C. | 2π+2$\sqrt{2}$-1 | D. | 2π+2$\sqrt{2}$ |
17.定义函数f(x)=2|x+5|-|x+1|,数列a1,a2,a3…满足an+1=f(an),n∈N*.若要使a1,a2,…an,…成等差数列.则a1的取值范围为( )
| A. | a1≥-5 | B. | a1≥-1 | C. | a1≥-1或a1≤-5 | D. | 以上都不对 |
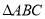 中,
中,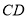 是
是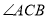 的角平分线,
的角平分线,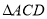 的外接圆交
的外接圆交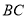 于
于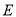 点.
点.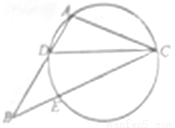
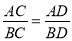 ;
;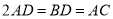 ,求
,求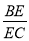 的值.
的值.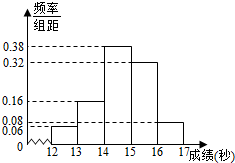 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图. 已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.
已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.