题目内容
已知椭圆中心 在坐标原点,焦点在
在坐标原点,焦点在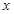 轴上,且经过
轴上,且经过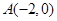 、
、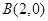 、
、 三点.
三点.
(1)求椭圆 的方程;
的方程;
(2)设直线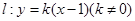 与椭圆
与椭圆 交于
交于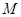 、
、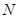 两点.
两点.
①若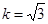 ,求
,求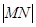 的长;
的长;
②证明:直线 与直线
与直线 的交点在直线
的交点在直线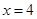 上.
上.
【答案】
解:(1)设椭圆方程为 ……1分
……1分
将 代入椭圆E的方程,得
代入椭圆E的方程,得
 ,解得
,解得 ∴椭圆
∴椭圆 的方程
的方程 ……3分
……3分
(2)

……5分
①若 ,则
,则
又 ……6分
……6分
 =
=
= ……8分
……8分
②

因此结论成立.直线 与直线
与直线 的交点住直线
的交点住直线 上.
……14分
上.
……14分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
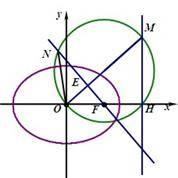 已知椭圆中心在坐标原点,短轴长为2,一条准线l的方程为x=2.
已知椭圆中心在坐标原点,短轴长为2,一条准线l的方程为x=2.