题目内容
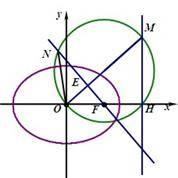 已知椭圆中心在坐标原点,短轴长为2,一条准线l的方程为x=2.
已知椭圆中心在坐标原点,短轴长为2,一条准线l的方程为x=2.(1)求椭圆方程;
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
分析:(1)由短轴和准线方程求出b和a的值,据焦点在x轴上写出椭圆的方程.
(2)用点斜式写出FN的方程,再由ON⊥NM,斜率之积等于-1得到一个等式,把FN的方程代入等式化简,
可得x2+y2=2,所以线段ON的长为定值
.
(2)用点斜式写出FN的方程,再由ON⊥NM,斜率之积等于-1得到一个等式,把FN的方程代入等式化简,
可得x2+y2=2,所以线段ON的长为定值
| 2 |
解答:解:(1)由题意知,b=1,
=2,∴a=
,c=1,焦点在x轴上,
∴椭圆的方程为
+y2=1.
(2)证明:∵F(1,0),点M(2,m),FN的方程为:y-0=
(x-1)①,
∵过点F作OM的垂线与以OM为直径的圆交于点N,
∴ON⊥NM,∴KON•KNM=-1,
即
•
=-1,∴x2+y2=2x+my ②,
把①代入②得:x2+y2=2x+my=2x+m•
(x-1)=2,
∴|ON|=
=
,∴线段ON的长为定值.
| a2 |
| c |
| 2 |
∴椭圆的方程为
| x2 |
| 2 |
(2)证明:∵F(1,0),点M(2,m),FN的方程为:y-0=
| -2 |
| m |
∵过点F作OM的垂线与以OM为直径的圆交于点N,
∴ON⊥NM,∴KON•KNM=-1,
即
| y |
| x |
| y-m |
| x-2 |
把①代入②得:x2+y2=2x+my=2x+m•
| -2 |
| m |
∴|ON|=
| x2+y2 |
| 2 |
点评:本题考查椭圆的方程、直线和圆的位置关系的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在坐标原点,焦点在
在坐标原点,焦点在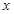 轴上,且经过
轴上,且经过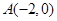 、
、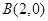 、
、 三点.
三点.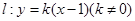 与椭圆
与椭圆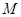 、
、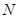 两点.
两点.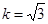 ,求
,求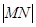 的长;
的长; 与直线
与直线 的交点在直线
的交点在直线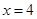 上.
上.