Question

【题目】已知定义在R上的偶函数满足：f（x+4）=f（x）+f（2），且当x∈[0，2]时，y=f（x）单调递减，给出以下四个命题：
①f（2）=0；
②x=﹣4为函数y=f（x）图象的一条对称轴；
③函数y=f（x）在[8，10]单调递增；
④若方程f（x）=m在[﹣6，﹣2]上的两根为x1 ， x2 ， 则x1+x2=﹣8．
上述命题中所有正确命题的序号为 ．

Answer 1

【答案】①②④
【解析】解：∵f（x）是定义在R上的偶函数，

∴f（﹣x）=f（x），

可得f（﹣2）=f（2），

在f（x+4）=f（x）+f（2），中令x=﹣2得

f（2）=f（﹣2）+f（2），

∴f（﹣2）=f（2）=0，

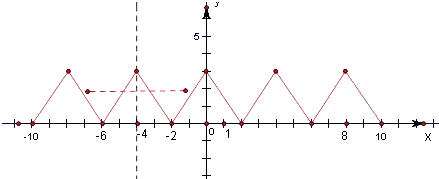
∴f（x+4）=f（x），∴函数f（x）是周期为4的周期函数，又当x∈[0，2]时，y=f（x）单调递减，结合函数的奇偶性画出函数f（x）的简图，如图所示．

从图中可以得出：

②x=﹣4为函数y=f（x）图象的一条对称轴；

③函数y=f（x）在[8，10]单调递减；

④若方程f（x）=m在[﹣6，﹣2]上的两根为x1，x2，则x1+x2=﹣8．

所以答案是：①②④．

【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识，掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系，以及对函数单调性的判断方法的理解，了解单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较．