题目内容
设正项数列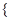 an
an 为等比数列,它的前n项和为Sn,a1=1,且
为等比数列,它的前n项和为Sn,a1=1,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)已知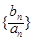 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列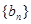 的前n项和Tn.
的前n项和Tn.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
 .
.
【解析】
试题分析:(Ⅰ)设在等比数列 中,公比为
中,公比为 , 根据
, 根据 .建立
.建立 的方程.
的方程.
(Ⅱ)由(I)可得 .从其结构上不难看出,应用“错位相减法”求和.
.从其结构上不难看出,应用“错位相减法”求和.
此类问题的解答,要特别注意和式中的“项数”.
试题解析:(Ⅰ)设在等比数列 中,公比为
中,公比为 ,
,
∵ ∴
∴ ∴
∴ 2分
2分
解得 或
或 4分
4分
所以 6分
6分
(Ⅱ)由已知得: ,则
,则 .
7分
.
7分

 ①
9分
①
9分
 ② 10分
② 10分
②—①,得




 12分
12分
考点:等比数列,“错位相减法”.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
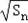 是an+2 和an的等比中项.
是an+2 和an的等比中项.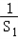 +
+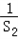 +…+
+…+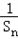 <1;
<1;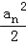 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个?