题目内容
12.已知△ABC中,AC=2,A=120°,cosB=$\sqrt{3}$sinC.(1)求边AB的长;
(2)设D是BC边上的一点,且△ACD的面积为$\frac{3\sqrt{3}}{4}$,求∠ADC的正弦值.
分析 (1)A=120°,cosB=$\sqrt{3}$sinC,求出tanC=$\frac{\sqrt{3}}{3}$,得出∴△ABC是以A为顶角的等腰三角形可得边AB的长;
(2)△ACD的面积为$\frac{3\sqrt{3}}{4}$,求出CD,根据勾股定理可求得AD,在△ADC中利用正弦定理,求∠ADC的正弦值.
解答  (1)在△ABC中,A=120°,
(1)在△ABC中,A=120°,
∴cosB=cos(π-A-C)=cos(60°-C)=$\frac{1}{2}$cosC+$\frac{\sqrt{3}}{2}$sinC①
∵cosB=$\sqrt{3}$sinC②.
联立①②可得$\frac{1}{2}$cosC+$\frac{\sqrt{3}}{2}$sinC=$\sqrt{3}$sinC
解得tanC=$\frac{\sqrt{3}}{3}$
∵在在△ABC中,A=120°
∴C<60°
∴C=30°
∴B=30°.
∴△ABC是以A为顶角的等腰三角形.
∴AB=2.
(2)如图,AE是等腰三角形ABC的高和中线,也是△ACD的高.
∵B=30°
∴在Rt△ABE中,AE=sin30°AB=1,BE=cos30•AB=$\sqrt{3}$
∴CE=$\sqrt{3}$
∵S△ACD=$\frac{3\sqrt{3}}{4}$
即$\frac{1}{2}$×CD×AE=$\frac{3\sqrt{3}}{4}$
∴CD=$\frac{3\sqrt{3}}{2}$
∴DE=CD-CE=$\frac{3\sqrt{3}}{2}$-$\sqrt{3}$=$\frac{\sqrt{3}}{2}$
∴在Rt△ADE中,AD=$\frac{1}{\sqrt{A{E}^{2}+D{E}^{2}}}$=$\frac{1}{\sqrt{(1)^{2}+(\frac{\sqrt{3}}{2})^{2}}}$=$\frac{2\sqrt{7}}{7}$
∵△ADC中,根据正弦定理可得:$\frac{AC}{sin∠ADC}$=$\frac{AD}{sin∠C}$
∴sin∠ADC=$\frac{\sqrt{7}}{2}$
点评 本题考查正弦定理的运用,考查三角形面积的计算,考查学生的计算能力,属于中档题.

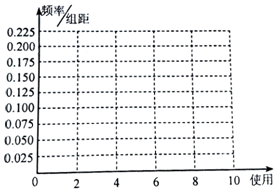 共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:| 使用时间 | [0,2] | (2,4] | (4,6] | (6,8] | (8,10] |
| 人数 | 10 | 40 | 25 | 20 | 5 |
(Ⅱ)作出这些数据的频率分布直方图;
(Ⅲ)估计该校大学生每周使用共享单车的平均时间$\overline t$(同一组中的数据用该组区间的中点值作代表).
 某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加x元,对应的销量y(万份)与x(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组x与y的对应数据:
| x(元) | 25 | 30 | 38 | 45 | 52 |
| 销售y(万册) | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
(i)求参数b的估计值;
(ii)若把回归方程$\hat y=10.0-bx$当作y与x的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
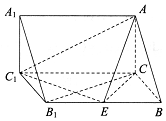 如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.
如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.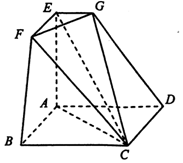 如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.