题目内容
14.正四棱锥的侧棱长是底面长的k倍,则k的取值范围是( )| A. | (0,+∞) | B. | ($\frac{1}{2}$,+∞}) | C. | ($\sqrt{2}$,+∞) | D. | ($\frac{{\sqrt{2}}}{2}$,+∞) |
分析 从棱锥顶点向底面正方形中心引一辅助线,该辅助线垂直底面,辅助线、侧棱与正方形对角线的一半构成直角三角形,
侧棱为斜边;根据直角三角形中的边角关系即可求出k的取值范围.
解答  解:如图所示,
解:如图所示,
设正四棱锥V-ABCD底面中心为O,BC=a,
则VB=ka,易知OB=$\frac{\sqrt{2}}{2}$a;
在Rt△VOB中,cos∠VBO=$\frac{\frac{\sqrt{2}}{2}a}{ka}$=$\frac{\sqrt{2}}{2k}$,
∵∠VBO∈(0,$\frac{π}{2}$),
∴0<$\frac{\sqrt{2}}{2k}$<1,
∴$\left\{\begin{array}{l}{k>0}\\{2k>\sqrt{2}}\end{array}\right.$,
解得k>$\frac{\sqrt{2}}{2}$;
∴k的取值范围是($\frac{\sqrt{2}}{2}$,+∞).
点评 本题考查了正四棱锥的结构特征的应用问题,也考查了空间想象能力与逻辑推理能力,是基础题目.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
9.已知f(x)=ex(sinx-cosx),则函数f(x)的图象x=$\frac{π}{2}$处的切线的斜率为( )
| A. | 2e | B. | ${e^{\frac{π}{2}}}$ | C. | e | D. | 2${e^{\frac{π}{2}}}$ |
19.设函数f(x)=cos(2x+$\frac{π}{4}$)+sin(2x+$\frac{π}{4}$),则( )
| A. | 函数f(x)在区间($\frac{π}{2},π$)内单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | 函数f(x)在区间($\frac{π}{2}$,π)内单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | 函数f(x)在区间($\frac{π}{2}$,π)内单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | 函数f(x)在区间($\frac{π}{2},π$)内单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
3.某工厂共有甲、乙、丙三个车间,甲车间有x名职工,乙车间有300名职工,丙车间有y名职工,现采用分层抽样的方法从该厂抽取容量为45人的样本,甲车间抽取20人,丙车间抽取10人,则该工厂共有的职工人数是( )
| A. | 600人 | B. | 800人 | C. | 900人 | D. | 1000人 |
4.执行如图所示的程序框图,如果输入的N=2016,那么输出的S=( )
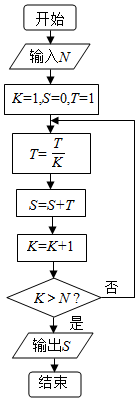

| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$ | B. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2015!}$ | ||
| C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2016}$ | D. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2016!}$ |
