题目内容
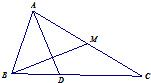
如图，△ABC中，已知∠BAC＝120°，AM是BC边上的中线，且AB＝4，AC＝6，求AM的长．
答案：
解析：
提示：
解析：
|
延长AM到点D，使MD＝AM，连结CD，BD，则四边形ABDC为平行四边形．在△ACD中，AC＝6，CD＝AB＝4，∠ACD＝180°－∠BAC＝60°．在△ACD中运用余弦定理得AD2＝AC2＋DC2－2AC·CD·cos∠ACD＝62＋42－2×6×4×cos60°＝28，所以AD＝
|
，AM＝
．
提示：
|
[提示]延长AM到点D，使MD＝AM，连结CD，BD，在△ABD中求出AD的长即可． [说明]在三角形中，已知两边及其夹角，求第三边，常运用余弦定理求解． |
练习册系列答案
相关题目
（1）已知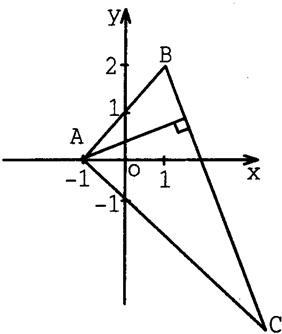
如图，△ABC中，已知A（-1，0），B（1，2），点B关于y=0的对称点在AC边上，且BC边上的高所在的直线方程为x-2y+1=0．
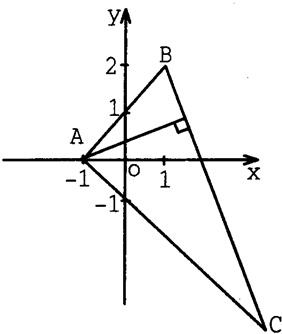如图，△ABC中，已知A（-1，0），B（1，2），点B关于y=0的对称点在AC边上，且BC边上的高所在的直线方程为x-2y+1=0．