题目内容
（1）已知tan(α+| π |
| 4 |
| sinα(3cosα-sinα) |
| 1+tanα |
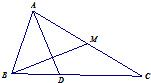
（2）如图：△ABC中，|
| AC |
| AB |
| DC |
| BD |
分析：（1）先把已知条件利用两角和与差的正切函数公式化简，然后通过观察所求的式子发现：分子分母中既有弦还有切，而已知条件只能求出正切，所以把原式里的正弦和余弦化切，即给分子分母都除以cos2α（分母还应根据弦切互化公式化弦），最后代入求值；
（2）要证明AD⊥BM，即要证明
•
=0，所以就要表示出
和
，利用三角形法则分别表示出即可．
（2）要证明AD⊥BM，即要证明
| AD |
| BM |
| AD |
| BM |
解答：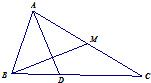
解：（1）∵tan(α+
)=-3，∴tanα=2
∴
=
=
（2）在三角形ABC中，利用三角形法则得
-
=
，
-
=
，
因为
=2
，代入求得：
=
+
；
因为M为AC的中点，所以
=
，而
-
=
，
-
=
，则有
=-
+
，
∴
•
=
(4|
|2-|
|2)=0，
∴AD⊥BM．
解：（1）∵tan(α+| π |
| 4 |
∴
| sinα(3cosα-sinα) |
| 1+tanα |
| 3tanα-tan2α |
| (1+tanα)(1+tan2α) |
| 2 |
| 15 |
（2）在三角形ABC中，利用三角形法则得
| AD |
| AB |
| BD |
| AC |
| AD |
| DC |
因为
| DC |
| BD |
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
因为M为AC的中点，所以
| AM |
| MC |
| BM |
| BA |
| AM |
| BC |
| BM |
| MC |
| BM |
| AB |
| 1 |
| 2 |
| AC |
∴
| AD |
| BM |
| 1 |
| 6 |
| AB |
| AC |
∴AD⊥BM．
点评：本题考查了两角和的正切函数公式，同角三角函数间的基本关系，以及先切互化公式，向量的表示法，让学生学会了用向量的方法证明两条线段的垂直，本题是一道多知识点的综合题，要求学生对每一个知识点都要灵活掌握和应用．
练习册系列答案
阅读快车系列答案
相关题目