题目内容
如图,△ABC中,已知A(-1,0),B(1,2),点B关于y=0的对称点在AC边上,且BC边上的高所在的直线方程为x-2y+1=0.(Ⅰ)求AC边所在直线的议程;
(Ⅱ)求点C的坐标.
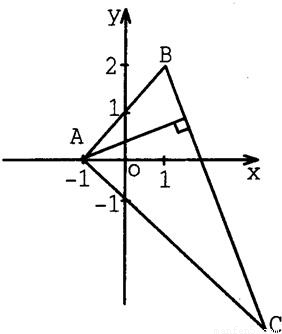
【答案】分析:(I)首先求出B的关于y=0的对称点B'(1,-2),然后根据B'点和A点求出直线方程;
(II)先求出直线BC的方程,然后根据图可知C点是直线AC和直线BC的交点,联立两方程即可求出结果.
解答:解:(I)点B关于y=0的对称点B'(1,-2)
∵A(-1,0),B'(1,-2),在AC边上
∴斜率k=-1
∴直线AC方程为y+2=-(x-1)即y+x+1=0
(II)∵BC边上的高所在的直线方程为x-2y+1=0
∴直线BC的斜率为-2
∴直线BC的方程为y-2=-2(x-1)即2x+y-4=0
∵C点是直线AC和直线BC的交点
∴
解得
∴点C的坐标为(5,-6)
点评:本题考查了直线方程的求法以及两直线交点的求法,解题过程要认真分析已知条件,属于基础题.
(II)先求出直线BC的方程,然后根据图可知C点是直线AC和直线BC的交点,联立两方程即可求出结果.
解答:解:(I)点B关于y=0的对称点B'(1,-2)
∵A(-1,0),B'(1,-2),在AC边上
∴斜率k=-1
∴直线AC方程为y+2=-(x-1)即y+x+1=0
(II)∵BC边上的高所在的直线方程为x-2y+1=0
∴直线BC的斜率为-2
∴直线BC的方程为y-2=-2(x-1)即2x+y-4=0
∵C点是直线AC和直线BC的交点
∴

解得

∴点C的坐标为(5,-6)
点评:本题考查了直线方程的求法以及两直线交点的求法,解题过程要认真分析已知条件,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)已知
(1)已知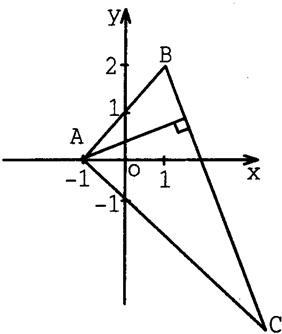 如图,△ABC中,已知A(-1,0),B(1,2),点B关于y=0的对称点在AC边上,且BC边上的高所在的直线方程为x-2y+1=0.
如图,△ABC中,已知A(-1,0),B(1,2),点B关于y=0的对称点在AC边上,且BC边上的高所在的直线方程为x-2y+1=0.
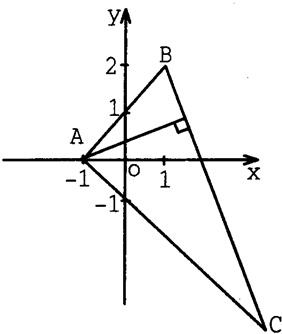 如图,△ABC中,已知A(-1,0),B(1,2),点B关于y=0的对称点在AC边上,且BC边上的高所在的直线方程为x-2y+1=0.
如图,△ABC中,已知A(-1,0),B(1,2),点B关于y=0的对称点在AC边上,且BC边上的高所在的直线方程为x-2y+1=0.