题目内容
【题目】
，
是两个平面，m，n是两条直线，有下列四个命题；
①如果
，
，
，那么
.
②如果，
，那么.
③如果
，
，那么
.
④如果
，，那么m与所成的角和n与所成的角相等.
其中正确的命题的个数为（ ）
A.1B.2C.3D.4
【答案】C
【解析】
对①，运用长方体模型，找出符合条件的直线和平面，即可判断；
对②，运用线面平行的性质定理和线面垂直的性质定理，即可判断；
对③，运用面面平行的性质定理，即可判断；
对④，由平行的传递性及线面角的定义，即可判断④．
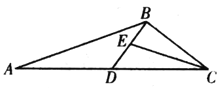
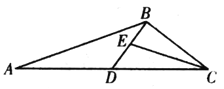
对于命题①，可运用长方体举反例证明其错误：如图，
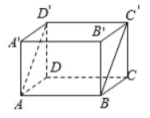
不妨设
为直线m，
为直线n，
所在的平面为
，
所在的平面为
，显然这些直线和平面满足题目条件，但
不成立；
命题②正确，证明如下：设过直线n的某平面与平面相交于直线l，则
，由
知
，从而
，结论正确；
由平面与平面平行的定义知命题如果
，
，那么
.③正确；
由平行的传递性及线面角的定义知命题：如果
，，那么m与所成的角和n与所成的角相等，④正确.
故选：C.
【题目】2019年4月，甲乙两校的学生参加了某考试机构举行的大联考，现对这两校参加考试的学生的数学成绩进行统计分析，数据统计显示，考生的数学成绩
服从正态分布
，从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷，并将这40份试卷的得分制作成如图所示的茎叶图：
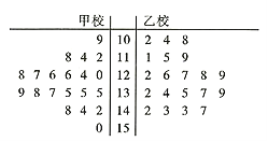
（1）试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数；
（2）若把数学成绩不低于135分的记作数学成绩优秀，根据茎叶图中的数据，判断是否有
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关？
（3）从所有参加此次联考的学生中（人数很多）任意抽取3人，记数学成绩在134分以上的人数为
，求的数学期望．
附：若随机变量服从正态分布
，则
，
，
．
参考公式与临界值表：
，其中
．
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
