Question

【题目】的内角、、的对边分别为，，，点为的中点，已知，，.

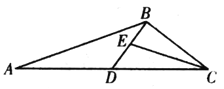
（1）求角的大小和的长；

（2）设的角平分线交于，求的面积.

Answer 1

【答案】（1）（2）

【解析】

（1）由三角函数恒等变换的应用化简已知等式可得tanC，结合范围C∈（0，π），可求C的值，由余弦定理可得BD的值．

（2）由（1）可知BD2+BC2＝4＝CD2，可求∠DBC，可得S△DBC，利用三角形的面积公式可求S△BCES△CED，代入S△BCE+S△CED＝S△BCD，即可解得S△CED的值．

（1）∵由题意可得：sinC+1﹣2sin20，

∴sinC+cos（A+B）＝0，

又A+B＝π﹣C，

∴sinC﹣cosC＝0，可得tanC，

∵C∈（0，π），

∴C，

∴在△BCD中，由余弦定理可得：BD2＝3+4﹣21，

解得：BD＝1，

（2）由（1）可知BD2+BC2＝4＝CD2，

∴∠DBC，

∴S△DBCBDBC，

∵CE是∠BCD的角平分线，

∴∠BCE＝∠DCE，

在△CEB和△CED中，S△BCE，

S△CED，

可得：，

∴S△BCES△CED，

∴代入S△BCE+S△CED＝S△BCD，（1）S△CED，

∴S△CED（2）＝23．