题目内容

计算：①1A₁¹+2A₂²+3A₃³+…+nA_nⁿ；② $数学公式$ ．

解：①1A₁¹+2A₂²+3A₃³+…+nA_nⁿ
=（A₂²-A₁¹）+（A₃³-A₂²）+…+（A_n+1ⁿ⁺¹-A_nⁿ）
=A_n+1ⁿ⁺¹-A₁¹；
②∵A_n+1ⁿ⁺¹-A_nⁿ=nA_nⁿ，
∴n= $\text{[math]}$ ，
$\text{[math]}$ = $\text{[math]}$ ，
∴ $\text{[math]}$ =1- $\text{[math]}$ + $\text{[math]}$
=1- $\text{[math]}$ ．
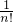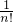分析：①本题考查的知识点是组合及组合数公式，要求1A₁¹+2A₂²+3A₃³+…+nA_nⁿ的值，我们根据A_n+1ⁿ⁺¹-A_nⁿ=nA_nⁿ对式子进行化简，不难求出1A₁¹+2A₂²+3A₃³+…+nA_nⁿ的值．
点评：此题是个中档题．考查用排列组合数公式的性质A_n+1ⁿ⁺¹-A_nⁿ=nA_nⁿ对式子进行化简是本题的关键，要求大家熟练掌握．

练习册系列答案

常德标准卷系列答案

超级奥赛培优竞赛系列答案

超级考卷系列答案

超级培优系列答案

超级英语系列答案

晨光全优同步指导训练与检测系列答案

成功宝典系列答案

成功中考系统总复习系列答案

成长记寒假总动员云南科技出版社系列答案

冲刺100分必备必练系列答案

相关题目

已知定义在R上奇函数f（x）=ax³+bx²+cx+d（a≠0），f（1）≠1；且当x∈[1，2]时，函数 $数学公式$ 的值域为[-2，1]．
（1）求函数f（x）的解析式；
（2）判断函数f（x）在x∈[1，+∞）上的单调性（不需写出推理过程），并写出f（x）在其定义域上的单调区间；
（3）讨论关于x的方程f（x）-t=0（t∈R）的根的个数．

与“a＞b”等价的不等式是

A.
|a|＞|b|
B.
a²＞b²
C.
a³＞b³
D.
$数学公式$ ＞1

已知函数f（x）是R上的单调增函数且为奇函数，则f（1）的值

A.
恒为正数
B.
恒为负数
C.
恒为0
D.
可正可负

已知a、b是正常数，若0＜x＜1，则函数f（x）= $数学公式$ 的最小值是________．

已知函数f（x）=-x²+4x-10（x≤2），若f（1-2^a）＞f（a），则实数a的取值范围是________．

关于x、y的二元一次方程组 $数学公式$ 无解，则m=________．

设f（x）= $数学公式$ （其中e为自然对数的底数），则 $数学公式$ 的值为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

i是虚数单位，复数 $数学公式$ =

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$