题目内容
3.已知|$\overrightarrow{a}$|=6,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,问当k取何值时,(k$\overrightarrow{a}$+$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$-2$\overrightarrow{b}$).分析 由向量垂直与数量积间的关系列式,展开数量积公式,化为关于k的一次方程求解.
解答 解:|$\overrightarrow{a}$|=6,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,
由(k$\overrightarrow{a}$+$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$-2$\overrightarrow{b}$),得(k$\overrightarrow{a}$+$\overrightarrow{b}$)•(3$\overrightarrow{a}$-2$\overrightarrow{b}$)=0,
即$k|\overrightarrow{a}{|}^{2}-2|\overrightarrow{b}{|}^{2}$$+(3-2k)\overrightarrow{a}•\overrightarrow{b}=0$,
即36k-8+(3-2k)×6×2×cos60°=0,
∴24k+10=0,即k=$-\frac{5}{12}$.
点评 本题考查平面向量的数量积运算,考查向量垂直与数量积间的关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.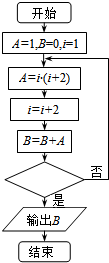 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )| A. | i≥13? | B. | i>14? | C. | i≥14? | D. | i≥15? |
13.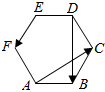 如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
 如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )| A. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$ |