题目内容
设△ABC的内角A,B,C所对的边长分别为a,b,c且acosB-bcosA= c、则
c、则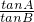 的值为________.
的值为________.
4
分析:先根据正弦定理得到sinAcosB-sinBcosA= sinC,再由两角和与差的正弦公式进行化简可得到sinAcosB=4sinBcosA,然后转化为正切的形式可得到答案.
sinC,再由两角和与差的正弦公式进行化简可得到sinAcosB=4sinBcosA,然后转化为正切的形式可得到答案.
解答:由acosB-bcosA= c及正弦定理可得
c及正弦定理可得
sinAcosB-sinBcosA= sinC,即sinAcosB-sinBcosA=
sinC,即sinAcosB-sinBcosA= sin(A+B),
sin(A+B),
即5(sinAcosB-sinBcosA)=3(sinAcosB+sinBcosA),
即sinAcosB=4sinBcosA,因此tanA=4tanB,
所以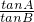 =4.
=4.
故答案为:4
点评:本题主要考查正弦定理的应用和切化弦的基本应用.三角函数的公式比较多,要注意公式的记忆和熟练应用.
分析:先根据正弦定理得到sinAcosB-sinBcosA=
 sinC,再由两角和与差的正弦公式进行化简可得到sinAcosB=4sinBcosA,然后转化为正切的形式可得到答案.
sinC,再由两角和与差的正弦公式进行化简可得到sinAcosB=4sinBcosA,然后转化为正切的形式可得到答案.解答:由acosB-bcosA=
 c及正弦定理可得
c及正弦定理可得sinAcosB-sinBcosA=
 sinC,即sinAcosB-sinBcosA=
sinC,即sinAcosB-sinBcosA= sin(A+B),
sin(A+B),即5(sinAcosB-sinBcosA)=3(sinAcosB+sinBcosA),
即sinAcosB=4sinBcosA,因此tanA=4tanB,
所以
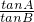 =4.
=4.故答案为:4
点评:本题主要考查正弦定理的应用和切化弦的基本应用.三角函数的公式比较多,要注意公式的记忆和熟练应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目