题目内容
如图，在矩形ABCD中，AB=6，BC=4，E是CD的中点，沿AE将△ADE折起，使二面角D-AE-B为60°，则四棱锥D-ABCE的体积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：作出四棱锥的高，在侧面ABD上的斜高，从而构造了二面角D-AE-B，计算出高和底的面积，再用棱锥的体积公式化求解．
解答：
解：如图，作DF⊥AE，DO⊥平面ABCD，连结OF，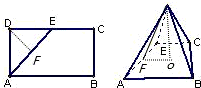
根据题意，∠DFO=60°，
在△ADE中，DF=
=
=
，
在△DFO中，DO=DF•sin60°=
，
S四边形ABCE=
(AB+CE)•BC=18，
∴四棱锥D-ABCE的体积：
V=
S四边形ABCE•DO=
×18×
=
．
故选：B．
根据题意，∠DFO=60°，
在△ADE中，DF=
| AD•DE |
| AE |
| 4×3 | ||
|
| 12 |
| 5 |
在△DFO中，DO=DF•sin60°=
6
| ||
| 5 |
S四边形ABCE=
| 1 |
| 2 |
∴四棱锥D-ABCE的体积：
V=
| 1 |
| 3 |
| 1 |
| 3 |
6
| ||
| 5 |
36
| ||
| 5 |
故选：B．
点评：本题考查四棱锥D-ABCE的体积的求法，考查平面图形和空间图形的转化，要注意前后的不变量和改变量．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
过棱长为a的正方体的三个顶点截下一个底面是等边三角形的棱锥，这个棱锥的表面积是（ ）
A、（3+
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=3x-2，x∈[-1，1]的值域是（ ）
A、[1，
| ||
| B、[-1，1] | ||
C、[-
| ||
| D、[0，1] |
马先生于两年前购买了一部手机，现在这款手机的价格已降为1000元，设这种手机每年降价20%，那么两年前这部手机的价格为（ ）
| A、1535.5元 |
| B、1440元 |
| C、1620元 |
| D、1562.5元 |
已知函数f（x）=
，满足对任意x1≠x2，都有
＜0，则实数a取值的范围是（ ）
|
| f(x1)-f(x2) |
| x1-x2 |
| A、1＜a＜3 |
| B、2≤a＜3 |
| C、1＜a≤2 |
| D、2＜a＜3 |
已知向量
，
，
，满足|
|=2，|
-
|=|
|，（
-
）•（
-
）=0，若对于每一确定的
，|
|的最大值和最小值分别为m，n，则对任意
，m-n的最小值是（ ）
| a |
| b |
| c |
| a |
| a |
| b |
| b |
| a |
| c |
| b |
| c |
| b |
| c |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
空中有一气球，在它的正西方A点测得它的仰角为45°，同时在它南偏东60°的B点，测得它的仰角为30°，若A、B两点间的距离为266米，这两个观测点均离地1米，那么测量时气球到地面的距离是（ ）
A、
| ||||
B、（
| ||||
| C、266米 | ||||
D、266
|