题目内容
如图2-12,已知⊙O和⊙O′都经过A、B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D.求证:AB2=BC·BD.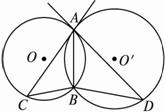
图2-12
思路分析:欲证AB2=BC·BD,即要证
=
,于是只要证△ABD∽△ABC即可,而题目中分别给出两圆切线,可产生弦切角定理,从而命题得证.
证明:∵AC是⊙O′的切线,AD是⊙O的切线,?
∴∠BAD =∠C,∠BAC =∠D.?
∴△ABD∽△CBA.?
∴
=
,即AB2=BC·BD.
练习册系列答案
相关题目
（2012•湖南模拟）为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．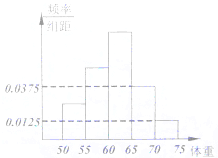
为了解某校男生体重情况，将样本数据整理后，画出其频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第3小组的频数为12，则样本容量是
,PB=CD=2,则BC∶AD的值为( )
B. 
C.
D.
