题目内容
如图2-12,已知AB是⊙O直径,P是AB延长线上的一点,PCD是割线,⊙O的半径为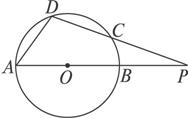
,PB=CD=2,则BC∶AD的值为( )
图2-12
A. 
B. 
C.
D.
解析:∵PAB、PCD是⊙O割线,
∴PB·PA=PC·PD.
∵⊙O的半径为
,PB=CD=2,
∴PA=PB+AB=.
∴PD=PC+CD=PC+2.
∴2×=PC(PC+2).
解得PC=3或-5(舍去).
∵ABCD是⊙O的内接四边形,
∴∠PBC=∠D.
又∵∠P=∠P,∴△ADP∽△CBP.
∴==.
答案:B
练习册系列答案
相关题目
为了了解高三学生的身体状况．抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12．则抽取的男生人数是（ ）
