[题目]设数列{an}满足．(1)若.求证:存在(a.b.c为常数).使数列是等比数列.并求出数列{an}的通项公式,(2)若an 是一个等差数列{bn}的前n项和.求首项a1的值与数列{bn}的通项公式．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设数列{an}满足．

（1）若，求证：存在（a，b，c为常数），使数列是等比数列，并求出数列{an}的通项公式；

（2）若an 是一个等差数列{bn}的前n项和，求首项a1的值与数列{bn}的通项公式．

【答案】（1）；（2），

【解析】

试题分析:（1）根据等比数列定义可得恒成立，根据对应项系数相等列方程组，解得各参数，再根据数列通项公式得{an}的通项公式；

（2）设，根据方程恒成立对应项系数相等列方程组，解得各参数，解得a1

最后根据等差数列求和公式逆推通项公式

试题解析：(1)证明：设数列{ an f(n) }的公比为，则：．

而

．

由等式恒成立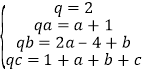得，解得．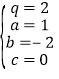

故存在，使数列{ an f(n) }成公比为2的等比数列．

又，所以．

所以．

(2) 因为an 是一个等差数列{bn}的前n项和，可设，则:

．

又an1 = 2an n2 4n 1 ．

由此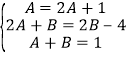得，解得．

所以，所以．

所以当时，．

当时，满足上式．

故．

练习册系列答案

相关题目

【题目】在四棱锥中，与相交于点，点在线段上，，且平面．

（1）求实数的值；

（2）若，, 求点到平面的距离．

【题目】设a为正实数．如图，一个水轮的半径为a m，水轮圆心 O 距离水面，已知水轮每分钟逆时针转动 5 圈．当水轮上的点 P 从水中浮现时（即图中点）开始计算时间．

（1）将点 P 距离水面的高度 h(m )表示为时间 t(s)的函数；

（2）点 P 第一次达到最高点需要多少时间．

【题目】已知椭圆：的离心率为，以短轴端点和焦点为顶点的四边形的周长为.

（Ⅰ）求椭圆的标准方程及焦点坐标.

（Ⅱ）过椭圆的右焦点作轴的垂线，交椭圆于、两点，过椭圆上不同于点、的任意一点，作直线、分别交轴于、两点.证明：点、的横坐标之积为定值.

【题目】若无穷数列满足：是正实数，当时，，则称是“-数列”.已知数列是“-数列”.

（Ⅰ）若，写出的所有可能值；

（Ⅱ）证明：是等差数列当且仅当单调递减；

（Ⅲ）若存在正整数，对任意正整数，都有，证明：是数列的最大项.

【题目】已知函数（且）．

（Ⅰ）当时，求函数的单调区间．

（Ⅱ）当时，，求的取值范围．

【题目】如图，四边形ABCD为矩形，平面ABCD⊥平面ABE，F为CE的中点，且AE⊥BE．

（1）求证：AE∥平面BFD：

（2）求证：BF⊥AE．

【题目】已知函数.

(1)若，求函数的单调区间；

(2)若的极小值点，求实数a的取值范围。

【题目】某同学用“五点法”画函数在某一周期内的图象时，列表并填入了部分数据，如下表：


			①

（1）请将上面表格中①的数据填写在答题卡相应位置上，并直接写出函数的解析式；

（2）若将函数的图象上所有点的横坐标变为原来的倍，纵坐标不变，得到函数的图象，求当时，函数的单调递增区间；

（3）若将函数图象上的所有点向右平移个单位长度，得到的图象. 若图象的一个对称中心为，求的最小值.

试题分类