题目内容
已知向量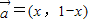
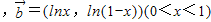 .
.(1)是否存在x,使得
 或
或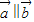 ?若存在,则举一例说明;若不存在,则证明之.
?若存在,则举一例说明;若不存在,则证明之.(2)求函数
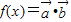 在区间
在区间 上的最值.(参考公式
上的最值.(参考公式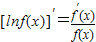 )
)
【答案】分析:(1)通过x= ,求出
,求出 的关系,得到
的关系,得到 ,计算
,计算 说明不垂直.
说明不垂直.
(2)求出向量的数量积,化简后求出函数的导数,利用导数值的符号求出函数的单调区间,求出函数的最值.
解答:解:(1)例如,当 时,
时,
 ,
,
因为0<x<1,所以0<1-x<1,lnx<0.ln(1-x)<0. ,从而
,从而 与
与 不垂直.
不垂直.
(2)函数
 ,
,
令
当 时,
时, ,f′(x)<0,f(x)在区间
,f′(x)<0,f(x)在区间 上是减函数:
上是减函数:
当 时,
时, ,f′(x)>0,f(x)在区间
,f′(x)>0,f(x)在区间 上是增函数;
上是增函数;
所以f(x)在 时取得最小值,且最小值
时取得最小值,且最小值 ,
,
又
故f(x)在 时取得最大值,且最大值
时取得最大值,且最大值 .
.
点评:本题考查向量的数量积的应用,考查函数的导数的应用,求出函数的最值是解题的关键.
 ,求出
,求出 的关系,得到
的关系,得到 ,计算
,计算 说明不垂直.
说明不垂直.(2)求出向量的数量积,化简后求出函数的导数,利用导数值的符号求出函数的单调区间,求出函数的最值.
解答:解:(1)例如,当
 时,
时,
 ,
,
因为0<x<1,所以0<1-x<1,lnx<0.ln(1-x)<0.
 ,从而
,从而 与
与 不垂直.
不垂直.(2)函数

 ,
,令

当
 时,
时, ,f′(x)<0,f(x)在区间
,f′(x)<0,f(x)在区间 上是减函数:
上是减函数:当
 时,
时, ,f′(x)>0,f(x)在区间
,f′(x)>0,f(x)在区间 上是增函数;
上是增函数;所以f(x)在
 时取得最小值,且最小值
时取得最小值,且最小值 ,
,又

故f(x)在
 时取得最大值,且最大值
时取得最大值,且最大值 .
.点评:本题考查向量的数量积的应用,考查函数的导数的应用,求出函数的最值是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
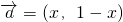
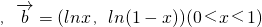 .
. 或
或 ?若存在,则举一例说明;若不存在,则证明之.
?若存在,则举一例说明;若不存在,则证明之. 在区间
在区间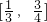 上的最值.(参考公式
上的最值.(参考公式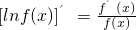 )
)